Negative Binomial in VBA21/9/2019
Have you ever tried to simulate a negative binomial random variable in a Spreadsheet?
If the answer to that is ‘nope – I’d just use Igloo/Metarisk/Remetrica’ then consider yourself lucky! Unfortunately not every actuary has access to a decent software package, and for those muddling through in Excel, this is not a particularly easy task. If on the other hand your answer is ‘nope – I’d use Python/R, welcome to the 21st century’. I’d say great, I like using those programs as well, but sometimes for reasons out of your control, things just have to be done in Excel. This is the situation I found myself in recently, and here is my attempt to solve it: Attempt 0 The first step I took in attempting to solve the problem was of course to Google it, then cross my fingers and hope that someone else has already solved it and this is just going to be a simple copy and paste. Unfortunately when I did search for VBA code to generate a negative binomial random variable, nothing comes up. In fact, nothing comes up when searching for code to simulate a Poisson random variable in VBA. Hopefully if you've found your way here, looking for this exact thing, then you're in luck, just scroll to the bottom and copy and paste my code. When I Googled it, there were a few solutions that almost solved the problem; there is a really useful Excel add-in called ‘Real statistics’ which I’ve used a few times: http://www.real-statistics.com/ It's a free excel add-in, and it does have functionality to simulate negative bimonials. If however you need someone to be able to re-run the Spreadsheet, they also will need to have it installed. In that case, you might as well use Python, and then hard code the frequency numbers. Also, I have had issues with it slowing Excel down considerably, so I decided not to use this in this case. I realised I’d have to come up with something myself, which ideally would meet the following criteria
How hard can that be? Attempt 1 I’d seen a trick before (from Pietro Parodi’s excellent book ‘Pricing in General Insurance’) that a negative binomial can be thought of as a Poisson distribution with a Gamma distribution as the conjugate prior. See the link below for more details: https://en.wikipedia.org/wiki/Conjugate_prior#Table_of_conjugate_distributions Since Excel has a built in Gamma inverse, we have simplified the problem to needing to write our own Poisson inverse. We can then easily generate negative binomials using a two step process:
Great, so we’ve reduced our problem to just being able to simulate a Poisson in VBA. Unfortunately there’s still no built in Poisson inverse in Excel (or at least the version I have), so we now need a VBA based method to generate this. There is another trick we can use for this - which is also taken from Pietro Parodi - the waiting time for a Poisson dist is an Exponential Dist. And the CDF of an Exponential dist is simple enough that we can just invert it and come up with a formula for generating an Exponential sample. We then set up a loop and add together exponential values, to arrive at Poisson sample. The code for this is give below:
Function Poisson_Inv(Lambda As Double)
s = 0
N = 0
Do While s < 1
u = Rnd()
s = s - (Application.WorksheetFunction.Ln(u) / Lambda)
k = k + 1
Loop
Poisson_Inv = (k - 1)
End Function
The VBA code for our negative binomial is therefore:
Function NegBinOld2(b, r)
Dim Lambda As Double
Dim N As Long
u = Rnd()
Lambda = Application.WorksheetFunction.Gamma_Inv(u, r, b)
N = Poisson_Inv(Lambda)
NegBinOld2 = N
End Function
Does this do everything we want?
There are a couple of downside of though:
This leads us on to Attempt 2 Attempt 2 If we pass the VBA a random uniform sample, then whenever we hit refresh in the Spreadsheet the random sample will refresh, which will force the Negative Binomial to resample. Without this, sometimes the VBA will function will not reload. i.e. we can use the sample to force a refresh whenever we like. Adapting the code gives the following:
Function NegBinOld(b, r, Rnd1 As Double)
Dim Lambda As Double
Dim N As Long
u = Rnd1
Lambda = Application.WorksheetFunction.Gamma_Inv(u, r, b)
N = Poisson_Inv(Lambda)
NegBinOld = N
End Function
So this solves the refresh problem. What about the random seed problem? Even though we now always get the same lambda for a given rand – and personally I quite like to hardcode these in the Spreadsheet once I’m happy with the model, just to speed things up. We still use the VBA rand function to generate the Poisson, this means everytime we refresh, even when passing it the same rand, we will get a different answer and this answer will be non-replicable. This suggests we should somehow use the first random uniform sample to generate all the others in a deterministic (but still pseudo-random) way. Attempt 3 The way I implemented this was to the set the seed in VBA to be equal to the uniform random we are passing the function, and then using the VBA random number generator (which works deterministically for a given seed) after that. This gives the following code:
Function NegBin(b, r, Rnd1 As Double)
Rnd (-1)
Randomize (Rnd1)
Dim Lambda As Double
Dim N As Long
u = Rnd()
Lambda = Application.WorksheetFunction.Gamma_Inv(u, r, b)
N = Poisson_Inv(Lambda)
NegBin = N
End Function
So we seem to have everything we want – a free, quick, solution that can be bundled in a Spreadsheet, which allows other people to rerun without installing any software, and we’ve also eliminated the forced refresh issue. What more could we want? The only slight issue with the last version of the negative binomial is that our parameters are still specified in terms of ‘b’ and ‘r’. Now what exactly are ‘b’ and ‘r’ and how do we relate them to our sample data? I’m not quite sure.... The next trick is shamelessly taken from a conversation I had with Guy Carp’s chief Actuary about their implementation of severity distributions in MetaRisk. Attempt 4 Why can't we reparameterise the distribution using parameters that we find useful, instead of feeling bound by using the standard statistics textbook definition (or even more specifically the list given in the appendix to ‘Loss Models – from data to decisions’, which seems to be somewhat of an industry standard), why can't we redefine all the parameters from all common actuarial distributions using a systematic approach for parameters? Let's imagine a framework where no matter which specific severity distribution you are looking at, the first parameter contains information about the mean (even better if it is literally scaled to the mean in some way), the second contains information about the shape or volatility, the third contains information about the tail weight, and so on. This makes fitting distributions easier, it makes comparing the goodness of fit of different distributions easier, and it make sense checking our fit much easier. I took this idea, and tied this in neatly to a method of moments parameterisation, whereby the first value is simply the mean of the distribution, and the second is the variance over the mean. This gives us our final version:
Function NegBin(Mean, VarOMean, Rnd1 As Double)
Rnd (-1)
Randomize (Rnd1)
Dim Lambda As Double
Dim N As Long
b = VarOMean - 1
r = Mean / b
u = Rnd()
Lambda = Application.WorksheetFunction.Gamma_Inv(u, r, b)
N = Poisson_Inv(Lambda)
NegBin = N
End Function
Function Poisson_Inv(Lambda As Double)
s = 0
N = 0
Do While s < 1
u = Rnd()
s = s - (Application.WorksheetFunction.Ln(u) / Lambda)
k = k + 1
Loop
Poisson_Inv = (k - 1)
End Function
If you have played around with Correlating Random Variables using a Correlation Matrix in [insert your favourite financial modelling software] then you may have noticed the requirement that the Correlation Matrix be positive semi-definite. But what exactly does this mean? And how would we check this ourselves in VBA or R? Mathematical Definition Let's start with the Mathematical definition. To be honest, it didn't really help me much in understanding what's going on, but it's still useful to know.
A symmetric $n$ x $n$ matrix $M$ is said to be positive semidefinite if the scalar $z^T M z $ is positive for every non-zero column vector $z$ of $n$ real numbers.
If I am remembering my first year Linear Algebra course correctly, then Matrices can be thought of as transformations on Vector Spaces. Here the Vector Space would be a collection of Random Variables. I'm sure there's some clever way in which this gives us some kind of non-degenerate behaviour. After a bit of research online I couldn't really find much. Intuitive Definition The intuitive explanation is much easier to understand. The requirement comes down to the need for internal consistency between the correlations of the Random Variables. For example, suppose we have three Random Variables, A, B, C. Let's suppose that A and B are highly correlated, that is to say, when A is a high value, B is also likely to be a high value. Let's also suppose that A and C are highly correlated, so that if A is a high value, then C is also likely to be a high value. We have now implicitly defined a constraint on the correlation between B and C. If A is high both B and C are also high, so it can't be the case that B and C are negatively correlated, i.e. that when B is high, C is low. Therefore some correlation matrices will give relations which are impossible to model. Alternative characterisations You can find a number of necessary and sufficient conditions for a matrix to be positive definite, I've included some of them below. I used number 2 in the VBA code for a real model I set up to check for positive definiteness. 1. All Eigenvalues are positive. If you have studied some Linear Algebra, then you may not be surprised to learn that there is a characterization using Eigenvalues. It seems like just about anything to do with Matrices can be restated in terms of Eigenvalues. I'm not really sure how to interpret this condition though in an intuitive way. 2. All leading principal minors are all positive This is the method I used to code the VBA algorithm below. The principal minors are just another name for the determinant of the upper-left $k$ by $k$ sub-matrix. Since VBA has a built in method for returning the determinant of a matrix this was quite an easy method to code. 3. It has a unique Cholesky decomposition I don't really understand this one properly, however I remember reading that Cholesky decomposition is used in the Copula Method when sampling Random Variables, therefore I suspect that this characterisation may be important! Since I couldn't really write much about Cholesky decomposition here is a picture of Cholesky instead, looking quite dapper. All 2x2 matrices are positive semi-definite Since we are dealing with Correlation Matrices, rather than arbitrary Matrices, we can actually show a-priori that all 2 x 2 Matrices are positive semi-definite. Proof
Let M be a $2$ x $2$ correlation matrix.
$$M = \begin{bmatrix} 1&a\\ a&1 \end{bmatrix}$$ And let $z$ be the column vector $M = \begin{bmatrix} z_1\\ z_2 \end{bmatrix}$ Then we can calculate $z^T M z$ $$z^T M z = {\begin{bmatrix} z_1\\ z_2 \end{bmatrix}}^T \begin{bmatrix} 1&a\\ a&1 \end{bmatrix} \begin{bmatrix} z_1\\ z_2 \end{bmatrix} $$ Multiplying this out gives us: $$ = {\begin{bmatrix} z_1\\ z_2 \end{bmatrix}}^T \begin{bmatrix} z_1 & a z_2 \\ a z_1 & z_2 \end{bmatrix} = z_1 (z_1 + a z_2) + z_2 (a z_1 + z_2)$$ We can then simplify this to get: $$ = {z_1}^2 + a z_1 z_2 + a z_1 z_2 + {z_2}^2 = (z_1 + a z_2)^2 \geq 0$$ Which gives us the required result. This result is consistent with our intuitive explanation above, we need our Correlation Matrix to be positive semidefinite so that the correlations between any three random variables are internally consistent. Obviously, if we only have two random variables, then this is trivially true, so we can define any correlation between two random variables that we like. Not all 3x3 matrices are positive semi-definite The 3x3 case, is simple enough that we can derive explicit conditions. We do this using the second characterisation, that all principal minors must be greater than or equal to 0.
Demonstration
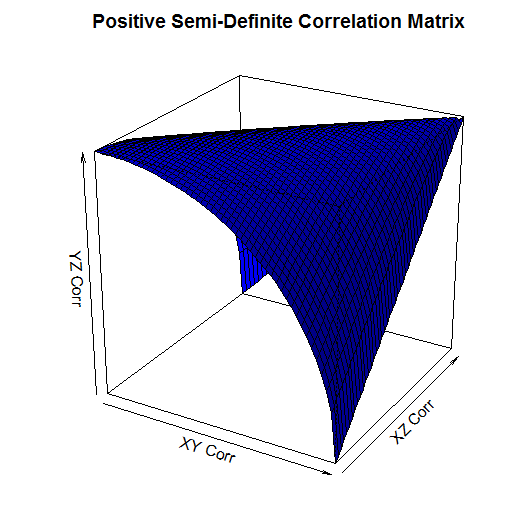
Let M be a $3$ x $3$ correlation matrix: $$M = \begin{bmatrix} 1&a&b\\ a&1&c \\ b&c&1 \end{bmatrix}$$ We first check the determinant of the $2$ x $2$ sub matrix. We need that: $ \begin{vmatrix} 1 & a \\ a & 1 \end{vmatrix} \geq 0 $ By definition: $ \begin{vmatrix} 1 & a \\ a & 1 \end{vmatrix} = 1 - a^2$ We have that $ | a | \leq 1 $, hence $ | a^2 | \leq 1 $, and therefore: $ | 1- a^2 | \geq 0 $ Therefore the determinant of the $2$ x $2$ principal sub-matrix is always positive. Now to check the full $3$ x $3$. We require: $ \begin{vmatrix} 1 & a & b \\ a & 1 & c \\ b & c & 1 \end{vmatrix} \geq 0 $ By definition: $ \begin{vmatrix} 1 & a & b \\ a & 1 & c \\ b & c & 1 \end{vmatrix} = 1 ( 1 - c^2) - a (a - bc) + b(ac - b) = 1 + 2abc - a^2 - b^2 - c^2 $ Therefore in order for a $3$ x $3$ matrix to be positive demi-definite we require: $a^2 + b^2 + c^2 - 2abc = 1 $ I created a 3d plot in R of this condition over the range [0,1].
It's a little hard to see, but the way to read this graph is that the YZ Correlation can take any value below the surface. So for example, when the XY Corr is 1, and the XZ Corr is 0, the YZ Corr has to be 0. When the XY Corr is 0 on the other hand, and XZ Corr is also 0, then the YZ Corr can be any value between 0 and 1. Checking that a Matrix is positive semi-definite using VBA When I needed to code a check for positive-definiteness in VBA I couldn't find anything online, so I had to write my own code. It makes use of the excel determinant function, and the second characterization mentioned above. Note that we only need to start with the 3x3 sub matrix as we know from above that all 1x1 and all 2x2 determinants are positive. This is not a very efficient algorithm, but it works and it's quite easy to follow.
Function CheckCorrMatrixPositiveDefinite()
Dim vMatrixRange As Variant
Dim vSubMatrix As Variant
Dim iSubMatrixSize As Integer
Dim iRow As Integer
Dim iCol As Integer
Dim bIsPositiveDefinite As Boolean
bIsPositiveDefinite = True
vMatrixRange = Range(Range("StartCorr"), Range("StartCorr").Offset(inumberofrisksources - 1, inumberofrisksources - 1))
' Only need to check matrices greater than size 2 as determinant always greater than 0 when less than or equal to size 2'
If iNumberOfRiskSources > 2 Then
For iSubMatrixSize = iNumberOfRiskSources To 3 Step -1
ReDim vSubMatrix(iSubMatrixSize - 1, iSubMatrixSize - 1)
For iRow = 1 To iSubMatrixSize
For iCol = 1 To iSubMatrixSize
vSubMatrix(iRow - 1, iCol - 1) = vMatrixRange(iRow, iCol)
Next
Next
'If the determinant of the matrix is 0, then the matrix is semi-positive definite'
If Application.WorksheetFunction.MDeterm(vSubMatrix) < 0 Then
CheckCorrMatrixisPositiveDefinite = False
bIsPositiveDefinite = False
End If
Next
End If
If bIsPositiveDefinite = True Then
CheckCorrMatrixPositiveDefinite = True
Else
CheckCorrMatrixPositiveDefinite = False
End If
End Function
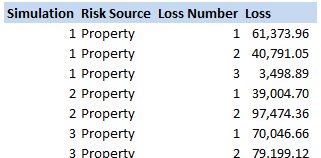
Checking that a Matrix is positive semi-definite in R Let's suppose that instead of VBA you were using an actually user friendly language like R. What does the code look like then to check that a matrix is positive semi-definite? All we need to do is install a package called 'Matrixcalc', and then we can use the following code: is.positive.definite( Matrix ) That's right, we needed to code up our own algorithm in VBA, whereas with R we can do the whole thing in one line using a built in function! It goes to show that the choice of language can massively effect how easy a task is. Compound Poisson Loss Model in VBA13/12/2017 I was attempting to set up a Loss Model in VBA at work yesterday. The model was a Compound-Poisson Frequency-Severity model, where the number of events is simulated from a Poisson distribution, and the Severity of events is simulated from a Severity curve. There are a couple of issues you naturally come across when writing this kind of model in VBA. Firstly, the inbuilt array methods are pretty useless, in particular dynamically resizing an array is not easy, and therefore when initialising each array it's easier to come up with an upper bound on the size of the array at the beginning of the program and then not have to amend the array size later on. Secondly, Excel has quite a low memory limit compared to the total available memory. This is made worse by the fact that we are still using 32-bit Office on most of our computers (for compatibility reasons) which has even lower limits. This memory limit is the reason we've all seen the annoying 'Out of Memory' error, forcing you to close Excel completely and reopen it in order to run a macro. The output of the VBA model was going to be a YLT (Yearly Loss Table), which could then easily be pasted into another model. Here is an example of a YLT with some made up numbers to give you an idea: It is much quicker in VBA to create the entire YLT in VBA and then paste it to Excel at the end, rather than pasting one row at a time to Excel. Especially since we would normally run between 10,000 and 50,000 simulations when carrying out a Monte Carlo Simulation. We therefore need to create and store an array when running the program with enough rows for the total number of losses across all simulations, but we won't know how many losses we will have until we actually simulate them. And this is where we come across our main problem. We need to come up with an upper bound for the size of this array due to the issues with dynamically resizing arrays, but since this is going to be a massive array, we want the upper bound to be as small as possible so as to reduce the chance of a memory overflow error. Upper Bound What we need then is an upper bound on the total number of losses across all the simulations years. Let us denote our Frequency Distribution by $N_i$, and the number of Simulations by $n$. We know that $N_i$ ~ $ Poi( \lambda ) \: \forall i$. Lets denote the total size of the YLT array by $T$. We know that $T$ is going to be: $$T = \sum_{1}^{n} N_i$$ We now use the result that the sum of two independent Poisson distributions is also a Poisson distribution with parameter equal to the sum of the two parameters. That is, if $X$ ~ $Poi( \lambda)$ , and $Y$ ~ $Poi( \mu)$, then $X + Y$ ~ $Poi( \lambda + \mu)$. By induction this result can then be extended to any finite sum of independent Poisson Distributions. Allowing us to rewrite $T$ as: $$ T \sim Poi( n \lambda ) $$ We now use another result, a Poisson Distribution approaches a Normally Distribution as $ \lambda \to \infty $. In this case, $ n \lambda $ is certainly large, as $n$ is going to be set to be at least $10,000$. We can therefore say that: $$ T \sim N ( n \lambda , n \lambda ) $$ Remember that $T$ is the distribution of the total number of losses in the YLT, and that we are interested in coming up with an upper bound for $T$. Let's say we are willing to accept a probabilistic upper bound. If our upper bound works 1 in 1,000,000 times, then we are happy to base our program on it. If this were the case, even if we had a team of 20 people, running the program 10 times a day each, the probability of the program failing even once in an entire year is only 4%. I then calculated the $Z$ values for a range of probabilities, where $Z$ is the unit Normal Distribution, in particular, I included the 1 in 1,000,000 Z value. We then need to convert our requirement on $T$ to an equivalent requirement on $Z$. $$ P ( T \leq x ) = p $$ If we now adjust $T$ so that it can be replaced with a standard Normal Distribution, we get: $$P \left( \frac {T - n \lambda} { \sqrt{ n \lambda } } \leq \frac {x - n \lambda} { \sqrt{ n \lambda } } \right) = p $$
Now replacing the left hand side with $Z$ gives:
$$P \left( Z \leq \frac {x - n \lambda} { \sqrt{ n \lambda } } \right) = p $$
Hence, our upper bound is given by:
$$T \lessapprox Z \sqrt{n \lambda} + n \lambda $$
Dividing through by $n \lambda $ converts this to an upper bound on the factor above the mean of the distribution. Giving us the following:
$$ T \lessapprox Z \frac {1} { \sqrt{n \lambda}} + 1 $$
We can see that given $n \lambda$ is expected to be very large and the $Z$ values relatively modest, this bound is actually very tight.
For example, if we assume that $n = 50,000$, and $\lambda = 3$, then we have the following bounds: So we see that even at the 1 in 1,000,000 level, we only need to set the YLT array size to be 1.2% above the mean in order to not have any overflow errors on our array. References (1) Proof that the sum of two independent Poisson Distributions is another Poisson Distribution math.stackexchange.com/questions/221078/poisson-distribution-of-sum-of-two-random-independent-variables-x-y
(2) Normal Approximation to the Poisson Distribution.
stats.stackexchange.com/questions/83283/normal-approximation-to-the-poisson-distribution |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|

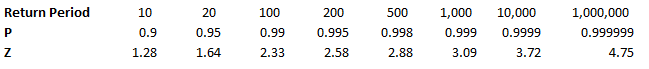
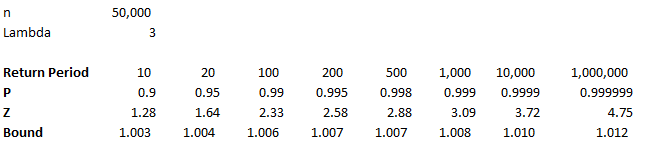
 RSS Feed
RSS Feed