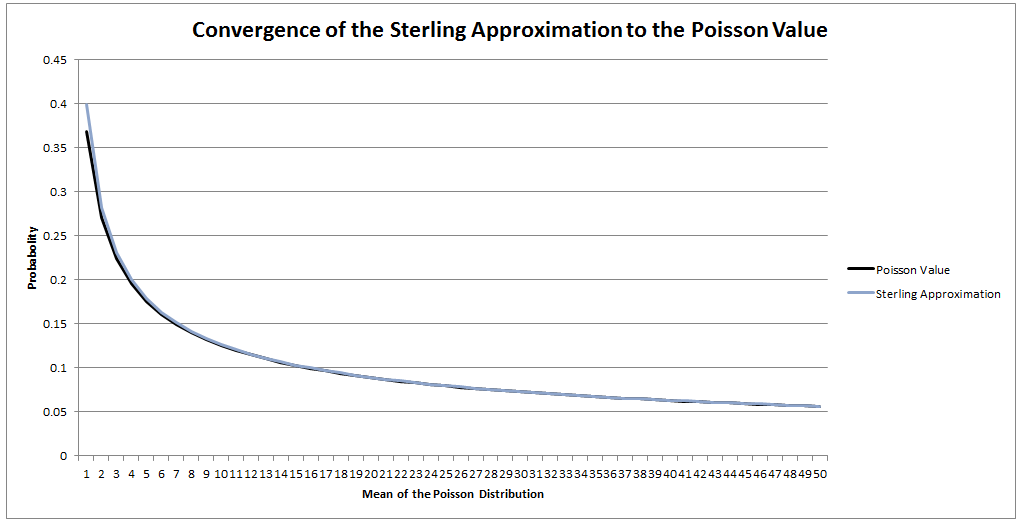
​I saw a cool trick the other day involving the Poisson Distribution and Stirling's Approximation.

Given a Poisson Distribution $ N  $ ~ $ Poi( \lambda ) $

The probability that $N$ is equal to a given $n$ is defined to be:

$$P ( N = n) = \frac { {\lambda}^n e^{-n} } {n! } $$
What is the probability that $N$ is equal to it's mean? In this case, let's use $n$ as the mean of the distribution for reasons that will become clear later.

Plugging $n$ into the definition of the Poisson distribution gives:

$$P ( N = n) = \frac { n^n e^{-n} } {n! } $$
At this point, we use Sterling's approximation. Which states that for large $n$:

                                                             $n!$  ~ $ {\left( \frac { n } {e } \right) }^n \frac { 1 } { \sqrt{ 2 \pi n } }$

Plugging this into the definition of the Poission Distribution gives:

$$P ( N = n) = \frac { n^n e^{-n} } {{\left( \frac { n } {e } \right) }^n} \frac { 1 } { \sqrt{ 2 \pi n } } $$
Which simplifies to:

$$P ( N = n) = \frac { 1 } { \sqrt{ 2 \pi n } } $$

So for large $n$ we end up with a nice result for the Probability that a Poisson Distribution will end up being equal to it's Expected Value.

Convergence

The convergence of the series is actually really quick. I checked the convergence for n between 1 and 50, and even by n=5, the approximation is very close, when I graphed it, the lines become indistinguishable very quickly.
​

The underlying contracts are all the same, but different groups have different names for them. I thought I would make a post explaining the differences.

Here are the names of the sub-types of Excess of Loss Reinsurance that are used in the London Market:

• Risk Excess
• Excess of Loss
• Cat XL
• Agg XL

(The descriptions given below just describe the basic functionality of the contracts. There will be a lot more detail in the contracts. It's always a good idea to read the slip if possible to properly understand the contract. Also, bear in mind that some people in the London Market might use these terms differently. This just represents what I would understand if someone said one of these terms to me in everyday work.)

Risk Excess (RXS)

The limit and attachment for this contract applies individually per risk rather than in aggregate per loss. (hence why it is called a Risk Excess) So if our RXS is 5m xs 1m and we have a loss involving two risks each of which is individually a 3m loss. The total recovery will be 4m = (3m-1m) + (3m - 1m)

​Excess of Loss (XoL)

The limit and attachment for this contract apply in aggregate per loss rather than individually per risk. So if our XoL is 5m xs 1m and we have a loss involving two risks each of which is individually a 3m loss. The total recovery will be 5m = (6m-1m)
​
Catastrophe XL (Cat XL)

The limit and attachment for this contract apply in aggregate for losses to all policies covered by the contract during the duration of a Catastrophe. So if our Cat XL is 500m xs 100m, and there is a Hurricane which causes insured losses of 300m, then the total recovery will be 200m = (300m - 100m)

Aggregate XL (Agg XL)

The limit and attachment for this contract apply in aggregate for losses to all policies covered by the contract. This will normally be all policies in a single class. So if our Agg XL is 50m xs 10m and covers an Insurer's Aviation account. If the total Aviation losses for the year are 30m. Then the total recovery will be 20m = (30m - 10m)

​The IFoA notes

The IFoA notes distinguish between three types of Excess of Loss contract.

• Risk Excess of Loss
• Aggregate Excess of Loss
• Catastrophe Excess of Loss

The definitions for Risk Excess of Loss and Catastrophe Excess of Loss are basically the same as those commonly used in the London Market. The IFoA definition of Aggregate Excess of Loss is different though. The Institute defines an Aggregate Excess of Loss Contract to be an Excess of Loss contract which aggregates losses across multiple risks in some way. This could be across all risks involved in one event, across all policies for a given year, across all losses in a given sub-class, etc. So our standard Excess of Loss contract which we defined above, which aggregates across all risks involved in a single loss, would be considered an example of an aggregate contract according to the IFoA definition! Don't go around Lloyd's calling it an Aggregate Excess of Loss though, people will get very confused.

The IFoA definitions are more logical than the ones used in the London Market, where there is an arbitrary distinction between two types of aggregation. Our standard XoL contract does aggregate losses, therefore why not call it an Agg XoL? The reason we do call it that is because everyone else does, which when talking about definitions is a pretty compelling reason, even if it is not the most logical name.

Wikipedia

The Wikipedia page for Reinsurance (link below) distinguishes between three types of Excess of Loss contract.
en.wikipedia.org/wiki/Reinsurance

• Per Risk Excess of Loss
• Catastrophe Excess of Loss
• Aggregate Excess of Loss

Per Risk Excess of Loss is once again defined consistently, and the Aggregate Excess of Loss is also consistent with the common usage in the London Market. However, in this case, our standard Excess of Loss contract now falls under the definition of a Catastrophe Excess of Loss Layer. The Wiki article defines a Cat Excess of Loss contract to be one that aggregates across an Occurrence or Event - where event can either be a catastrophe, such as a Hurricane, or a single loss involving multiple risks.

Summary

You shouldn't get caught up in who is right or wrong, as long as you are clear which definitions you are using. Fundamentally we are talking about the same underlying contracts, it's all just semantics. The definitions that are commonly used in the London Market  are not online anywhere that I could see, and it caused me some confusion when I noticed the inconsistency did some googling, and nothing came up. Hopefully this helps clarify the situation to anyone else who gets confused in the future.