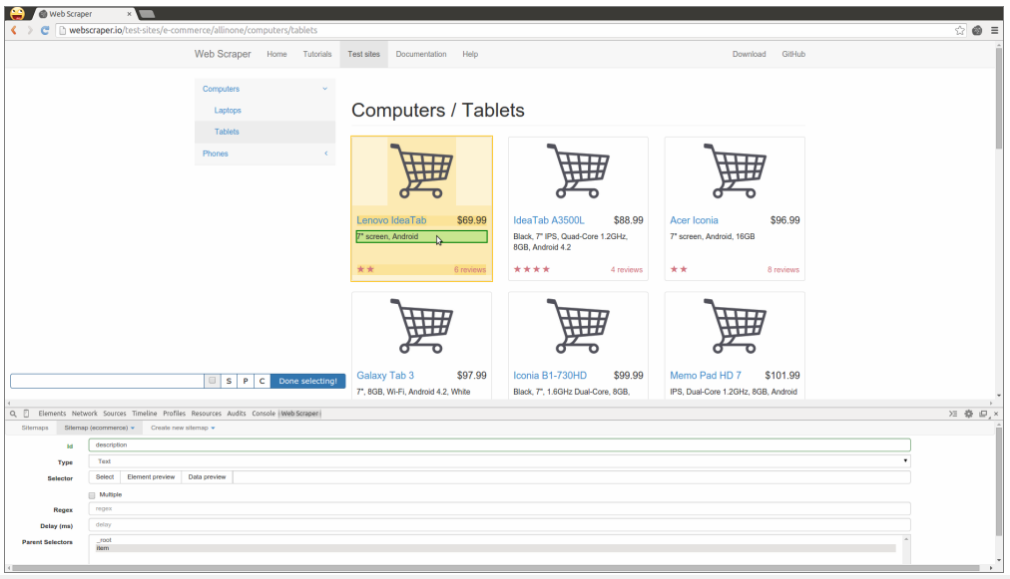
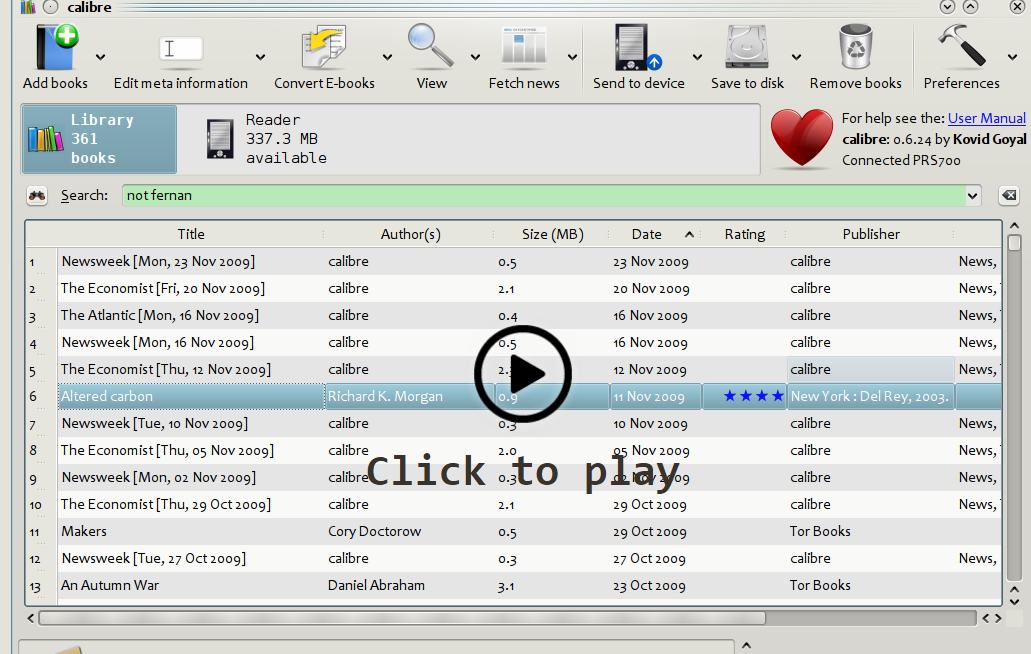
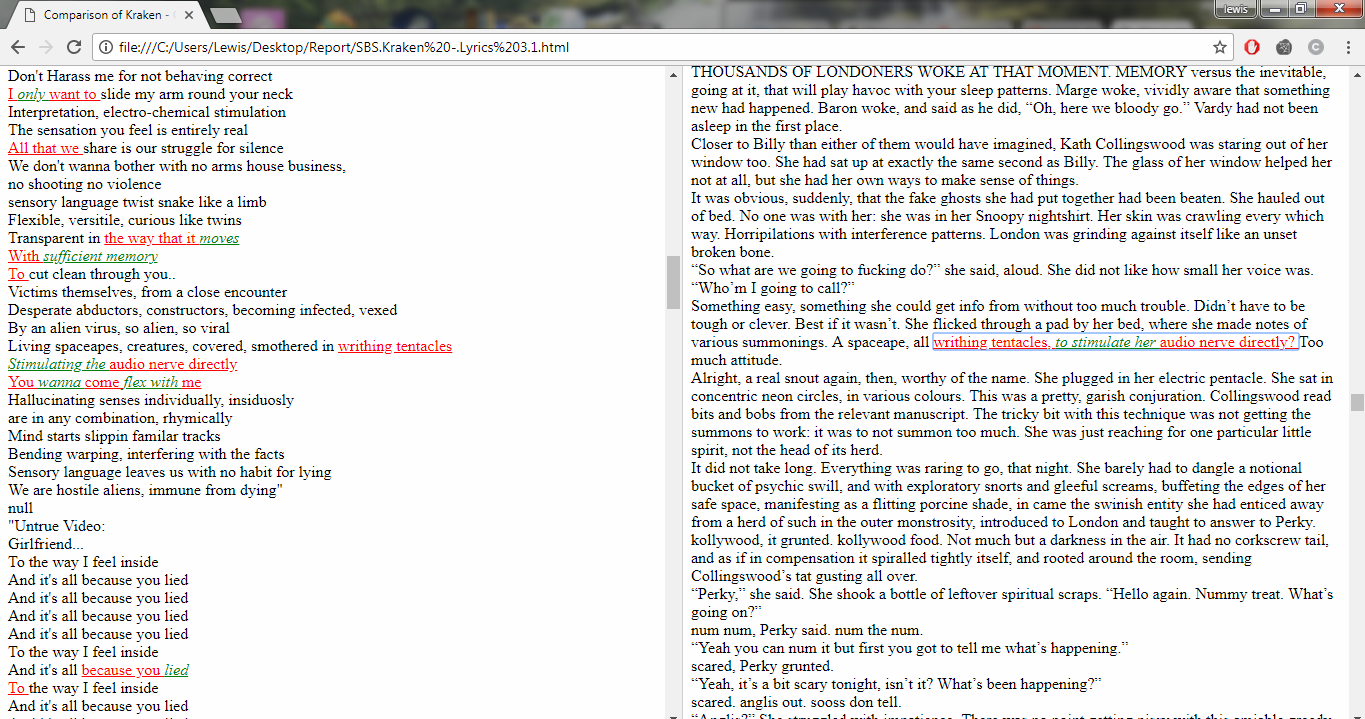
Song Lyrics in China Mieville Novels8/3/2018 I just finished reading China Mieville's novel Kraken. It was really cool, it did take me a while to get into Mieville's voice, but once I got into the swing of it I really enjoyed it. Here is the blurb in case you are interested: "In the Darwin Centre at London’s Natural History Museum, Billy Harrow, a cephalopod specialist, is conducting a tour whose climax is meant to be the Centre’s prize specimen of a rare Architeuthis dux--better known as the Giant Squid. But Billy’s tour takes an unexpected turn when the squid suddenly and impossibly vanishes into thin air." One of the lines in the book struck me as surprisingly familiar. Here is the quote from the book: "She flicked through a pad by her bed, where she made notes of various summonings. A spaceape, all writhing tentacles, to stimulate her audio nerve directly? Too much attitude." After thinking about this for a moment, it clicked that this is a reference to a Burial song called Spaceape (from his self titled album). The line goes: "Living spaceapes, creatures, covered, smothered in writhing tentacles Stimulating the audio nerve directly" I couldn't find any reference online to the inclusion of Burial lyrics in Mieville's novels. Okay I thought, that's a cool a easter egg, but it got my thinking, are there any other song lyrics buried in Mieville's books? And if so, is there any way we can scan them automatically? Collecting Lyrics The first step was to get a database of song lyrics which we can use to scan the novels for, Unfortunately there is no easy place to find a database of song lyrics, so I was forced to scrape them from a lyrics site. I used the following free chrome extension web scraper which is very easy to use, and in my experience very reliable: webscraper.io/ After about 10 minutes of setting it up, and about an hour of leaving it to run. I had managed to scrape most of Burial's lyrics in to csv files. I also scraped lyrics by Kode9 and Spaceape so I could see if they were referenced anywhere. It's hard to know which artist I should look for, but both of these have been mentioned by Mieville in interviews. The web scraping add-in has an easy to use GUI. Here is a screenshot of what it looks like to set it up: Ebooks in text format The next step was then to get his ebooks into a format that I could easily analyse. I assumed that I would need them in a csv format, but I actually got away with using .txt in the end. In order to get them into .txt. I used the built-in bulk converter in the following free ebook management program: calibre-ebook.com/ Here is a screenshot of Calibre. It is also very easy to use, and freely available online. Analysing the text This is now the hardest part of the problem. We have electronic copies of China Mieville's novels in .txt format, and we have a collection of lyrics in .txt format which we would like to compare them against, how can we programmatically analyse whether Mieville references other Burial lyrics in one of his books? If we simply attempt to match entire strings, then we have the issue that we might miss out on some references due to small changes in word ordering or punctuation. For example, in the example above using Burial's Spaceape, the wording is slightly different and the tenses of some of the words have been changed, therefore looking for an exact match between lyrics and text will probably not work. If on the other hand we don't match complete strings, but just try to match words, then we will be overwhelmed by small words like 'the' and 'a' which will be used multiple times in both Burial's song lyrics, and in China Mieville's novels. There are two main approaches I came up with.to solve this problem. My first thought was to match individual words, generating a huge list of matches, and then to count the number of uses of each word in Mieville's novels, and then sorting by the words that match but which are also the most uncommon. For example I would imagine that Spaceape is only ever used once in all of Mieville's novels, giving us information about how unusual this word is. Combined with the fact that this word is also used in a Burial lyric, gives us enough information to assume that there is a high probability of a match, at this point we could investigate manually. I ultimately didn't go down this road. Instead, I had the idea to try to adapt plagiarism detection software to this problem. When you think about it, the two problems are actually quite similar. Plagiarism detection is about trying to automatically check two documents for similar phrases, without relying on complete matches. Open Source Plagiarism Detection I found the following free-to-use program created by Lou Bloomfield of the University of Virginia which is perfect for what I was trying to do. plagiarism.bloomfieldmedia.com/wordpress/ It compares two sets of files and then creates a side by side hyperlinked comparison, which can be viewed in chrome, highlighting the parts of the documents where a possible match has been detected. There are various settings you can tweak to specify how close of a match you are interested in. I have included a screenshot below of the section where the Spaceape line is detected. There were about 500 matches detected when I ran this, but it only took about a minute to scroll through and check up on the ones that looked significant. Results Ultimately, this analysis felt like a bit of a failure. These were the only lyrics I could find in all of his novels and while there is always the chance that I need to expand the number of artists I'm looking at, or refine my detection methods I imagine this is all there is. I still thought the process was quite cool so I thought I'd write up what I had done anyway. If you have any thoughts, let me know by leaving a comment. Drinking Game Analysis3/3/2018
When you are playing a drinking game, do you ever catch yourself calculating the probabilities of various events happening? If you are like most people the answer to that is probably "..... um..... no....... why would I ever do that...."
Okay, maybe that's not the kind of thing you think about when playing a drinking game. But I bet you think it would be interesting to know what the odds are anyway? No? Really? Still not that interested? .... Okay... well I find it interesting, so I'm going to write about it anyway. Eyes up/Eyes down I've only played this game a couple of times but it's pretty fun, it requires no equipment, and has quite a lot of drinking. All players sit in a circle, one player calls out "Eye's down" at which point everyone looks down, the same player then says "Eye's up" at which point everyone looks up at a random person in the circle. If the person you are looking at is also looking at you, then you both drink. Pretty simple. What is the probability that you will drink? Let's denote the event that you have matched someone with $M$. Then: $$P(M) = \frac{1}{n-1} $$ Where $n$ is the number of players.
To see that this is true, assume that everyone is picking a random person to look at, then it shouldn't matter who you are looking at, that person will always have $n-1$ people to pick from, and therefore a $ \frac{1}{n-1} $ chance of looking at you.
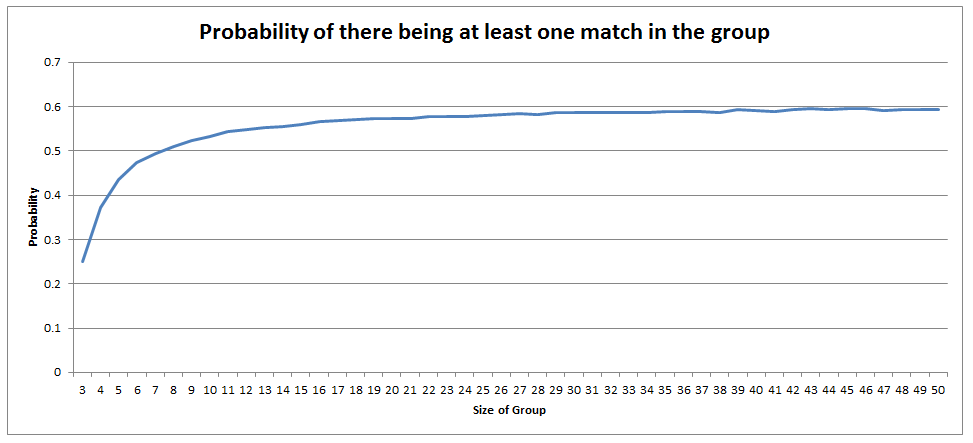
Of course people in real life tend not to pick a random person to look at, and even if they attempt to pick a random person, people have been shown to be terrible at picking randomly. But for the purposes of this analysis, unless we make this assumption, the only alternative would be to play the game hundreds of times, record how often matches are made, and then make an empirical claim. As fun as it sounds to play this game hundreds of times in a row, it would be better for your health to just assume a uniform spread of guesses. The fact that you have a $ \frac{1}{n-1} $ chance of getting a match means that the more people are playing the game, the less likely each person is to drink. Does this apply to the group as a whole though? What is the probability that someone in the group drinks? If we had a hundred people playing, then each individual would hardly ever drink. In fact you would expect them to drink once every $99$ goes. But would you expect it to also be unlikely that anyone at all drinks? I spent about an hour trying to calculate this and didn't get very far. Calculating through conditional probabilities doesn't seem to help, and I couldn't come up with a decent approach to count the permutations of all the possible ways of selecting pairings for elements in a set, such that there are no 2-cycles. In the end I gave up and just wrote a program to calculate the answer stochastically. Monte Carlo analysis really is such a versatile tool for problems like these. Anytime you can formulate the problem easily, but struggle to come up with an analytical solution, Monte Carlo analysis will probably work. Here is the table I generated of the probability of someone in the group drinking for a group of size n:
There is a definite trend here, if we plot the values on the chart it looks pretty clear that out solution converges to $0.6$. No idea why though! I might come back to this problem another time, but if anyone has any thoughts then please let me know.
Odds So this is not technically a drinking game, but is played quite often by people who are out drinking. The rules for this game are pretty simple, anytime you would like to dare someone to do something you say "odds of you doing this". The dare might be anything, from 'eating a spoon full of chilli powder, downing your drink, or even getting a tattoo (that last one is a real one I heard about from a friend who playing the game while travelling in Eastern Europe). The person you have challenged then gives you a number. They might say $20$, then each of you count down from $3$ and say an integer from $1$ to $20$ (or whatever number they selected). If you both said the same number, then they have to do the dare. Therefore the higher number you pick, the less likely it is that you will have to do the dare. What are the odds of you having to do whatever it is you are betting on, based on you selecting the number $n$? This is quite a straightforward problem, the answer is just $\frac{1} {n} $. I was playing this game last week with someone who thought the answer might be $\frac{1} {n^2} $. This would give a very different likelihood of having to do the dare. For example if you selected $20$, then you would have a $5 \%$ chance of having to do the dare, but according to my friend's calculation he thought you would have $0.25 \%$ chance of doing the dare. Here is a table showing the correct probabilities for various values of $n$. Dirty Pint Flip I wouldn't recommend playing this game to be honest. I played it in uni once, but it's a bit grim. All the players sit in a circle with a central pint glass in the middle, the players take it in turn to pour any amount of their own drink into the central pint glass as they would like, they then have to flip a coin and guess whether it will be heads or tails. If they get it right, then the game moves on to the person to their left, if they get it wrong, then they have to down the dirty pint. When I played it some people were drinking wine, some people were drinking beer... it was not a good combination. What is the probability that you will have to drink? This is quite straight forward, it is simply the probability that you will guess the coin flip correctly. Which is just $\frac{1}{2} $. What about the question of how much you will drink on average? That is, on average if you have to drink, how many people will have poured their drink into the glass before you drink? We can model this as a geometric distribution and calculate the probabilities of each possible number of people. Let's denote the number of people who have poured in before you, given you are about to drink as $N$, then:
$$N \sim Geo(0.5) $$
Giving us the following table: The expected value of the number of drinks is then the sumproduct of these two columns . This gives us a value of $2$. Therefore, if you have to drink, the average number of drinks that will have been poured into the pint is $2$. Two Dice Nominate This is another game I've only played a couple of times. And I'm not sure if it has a better name than the one I've given it, if you know of one then let me know. In this game, you sit in a circle with a range of drinks on the table, you take it in turns to nominate a person, a drink, and a number between $2$ and $12$. You then roll two dice and add them together. If you have rolled the correct number, the person you nominated drinks the drink you selected, if however you roll a double, then you drink that drink. If it is both a double and you get it correct, then you both have to drink. The reason that this game does not have much depth to it is that you can always just pick the most likely number to come up when rolling two dice. Here is a table showing the probability of each value coming up: Therefore you might as well pick $7$ every single time! Is there anything else we can say about this game? We know that if we roll a double, then we have to drink the drink. What is the probability of you rolling a double in this game? The probability of this is always just $\frac{1}{6} $. Interesting this is the same probability as rolling the dice such that the sum is $7$. Therefore, if you do pick $7$, there is an equal chance of you and the person you are nominating drinking the drink. |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
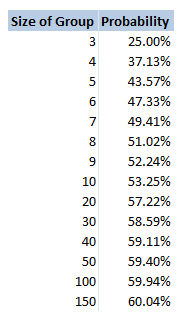
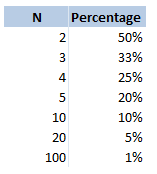
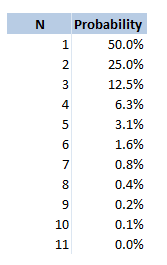
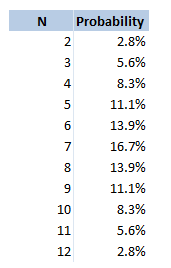
 RSS Feed
RSS Feed