|
I could be on my own here, but personally I always thought the definition of Sample Standard Deviation is pretty ugly. $$ \sqrt {\frac{1}{n - 1} \sum_{i=1}^{n} { ( x_i - \bar{x} )}^2 } $$ We've got a square root involved which can be problematic, and what's up with the $\frac{1}{n-1}$? Especially the fact that it's inside the square root, also why do we even need a separate definition for a sample standard deviation rather than a population standard deviation? When I looked into why we do this, it turns out that the concept of sample standard deviation is actually a bit of a mess. Before we tear it apart too much though, let's start by looking at some of the properties of standard deviation which are good. Advantages of Standard Deviation
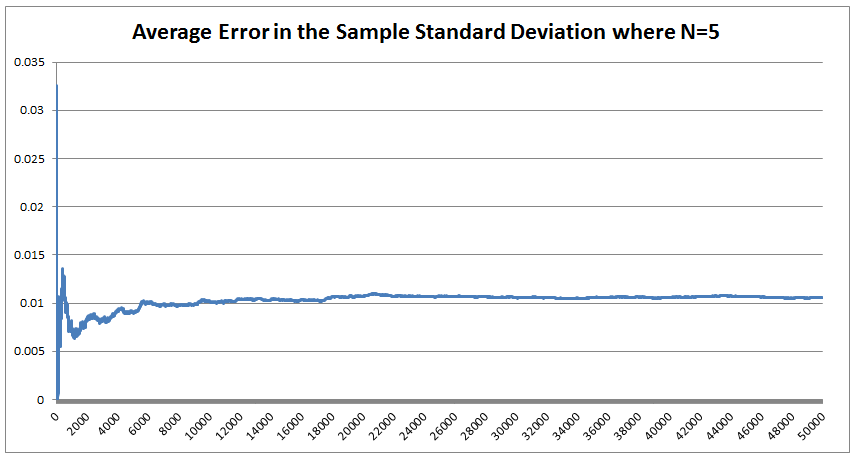
The last property is a really important one. The $\frac{1}{n-1}$ factor is a correction we make which we are told turns the sample standard deviation into an unbiased estimator of the population standard deviation. We can test this pretty easily, I sampled 50,000 simulations from a probability distribution and then measured the squared difference between the mean of the sample standard deviation and the actual value computed analytically. We see that the Average Error converges quite quickly but for some reason it doesn't converge to 0 as expected! It turns out that the usual formula for the sample standard deviation is not actually an unbiased estimator of the population standard deviation after all. I'm pretty sure they never mentioned that in my stats lectures at uni. The $n-1$ correction changes the formula for sample variance into an unbiased estimator, and the formula we use for the sample standard deviation is just the square root of the unbiased estimator for variance. If we do want an unbiased estimator for the sample standard deviation then we need to make an adjustment based not just on the sample size, but also the underlying distribution. Which in many cases we are not going to know at all. The wiki page has a good summary of the problem, and also has formulas for the unbiased estimator of the sample standard deviation: en.wikipedia.org/wiki/Unbiased_estimation_of_standard_deviation Just to give you a sense of the complexity, here is the factor that we need to apply to the usual definition of sample standard deviation in order to have an unbiased estimator for a normal distribution. $$ \frac {1} { \sqrt{ \frac{2}{n-1} } \frac{ \Gamma \Big( \frac{ n } {2} \Big) } {\Gamma \Big( \frac{n-1}{2} \Big)} } $$ Where $\Gamma$ is the Gamma function. Alternatives to Standard Deviation Are there any obvious alternatives to using standard deviation as our default measure of variability? Nassim Nicholas Taleb, author of Black Swan, is also not a fan of the wide spread use of the standard deviation of a distribution as a measure of its volatility. Taleb has different issues with it, mainly around the fact that it was often overused in banking by analysts who thought it completely characterised volatility. So for example, when modelling investment returns, an analyst would look at the sample standard deviation, and then assume the investment returns follow a Lognormal distribution with this standard deviation, when we should actually be modelling returns with a much fatter tailed distributions. So his issue was the fact that people believed that they were fully characterising volatility in this way, when they should have also been considering kurtosis and higher moments or considering fatter tailed distributions. Here is a link to Taleb's rant which is entertaining as always: www.edge.org/response-detail/25401 Taleb's suggestion is a different statistic called Mean Absolute Deviation the definition is. $$\frac{1}{n} \sum_{i=1}^n | x_i - \bar{x} | $$ We can see immediately why mathematicians prefer to deal with the standard deviation instead of the mean absolute deviation, working with sums of absolute values is normally much more difficult analytically than working with the square root of the sum of squares. In the ages of ubiquitous computing though, this should probably be a smaller consideration. Designing a new number system I got interested in alternative number systems when I read Malcolm Gladwell's book Outliers back in uni. You might be surprised that Gladwell would write about this topic, but he actually uses it to attempt to explain why Asian students tend to do so well at maths in the US. I was flicking through an old notebook the other day and I can across my attempt at designing such a system. I thought it might be interesting to write up my system. To set the scene, here is the relevant extract from the book: "Take a look at the following list of numbers: 4,8,5,3,9,7,6. Read them out loud to yourself. Now look away, and spend twenty seconds memorizing that sequence before saying them out loud again.If you speak English, you have about a 50 percent chance of remembering that sequence perfectly If you’re Chinese, though, you’re almost certain to get it right every time. Why is that? Because as human beings we store digits in a memory loop that runs for about two seconds. We most easily memorize whatever we can say or read within that two second span. And Chinese speakers get that list of numbers—4,8,5,3,9,7,6—right every time because—unlike English speakers—their language allows them to fit all those seven numbers into two seconds. That example comes from Stanislas Dehaene’s book “The Number Sense,” and as Dehaene explains: Chinese number words are remarkably brief. Most of them can be uttered in less than one-quarter of a second (for instance, 4 is ‘si’ and 7 ‘qi’) Their English equivalents—”four,” “seven”—are longer: pronouncing them takes about one-third of a second. The memory gap between English and Chinese apparently is entirely due to this difference in length. In languages as diverse as Welsh, Arabic, Chinese, English and Hebrew, there is a reproducible correlation between the time required to pronounce numbers in a given language and the memory span of its speakers. In this domain, the prize for efficacy goes to the Cantonese dialect of Chinese, whose brevity grants residents of Hong Kong a rocketing memory span of about 10 digits. It turns out that there is also a big difference in how number-naming systems in Western and Asian languages are constructed. In English, we say fourteen, sixteen, seventeen, eighteen and nineteen, so one would think that we would also say one-teen, two-teen, and three-teen. But we don’t. We make up a different form: eleven, twelve, thirteen, and fifteen. Similarly, we have forty, and sixty, which sound like what they are. But we also say fifty and thirty and twenty, which sort of sound what they are but not really. And, for that matter, for numbers above twenty, we put the “decade” first and the unit number second: twenty-one, twenty-two. For the teens, though, we do it the other way around. We put the decade second and the unit number first: fourteen, seventeen, eighteen. The number system in English is highly irregular. Not so in China, Japan and Korea. They have a logical counting system. Eleven is ten one. Twelve is ten two. Twenty-four is two ten four, and so on. That difference means that Asian children learn to count much faster. Four year old Chinese children can count, on average, up to forty. American children, at that age, can only count to fifteen, and don’t reach forty until they’re five: by the age of five, in other words, American children are already a year behind their Asian counterparts in the most fundamental of math skills. The regularity of their number systems also means that Asian children can perform basic functions—like addition—far more easily. Ask an English seven-year-old to add thirty-seven plus twenty two, in her head, and she has to convert the words to numbers (37 + 22). Only then can she do the math: 2 plus 7 is nine and 30 and 20 is 50, which makes 59. Ask an Asian child to add three-tens-seven and two tens-two, and then the necessary equation is right there, embedded in the sentence. No number translation is necessary: It’s five-tens nine. “The Asian system is transparent,” says Karen Fuson, a Northwestern University psychologist, who has done much of the research on Asian-Western differences. “I think that it makes the whole attitude toward math different. Instead of being a rote learning thing, there’s a pattern I can figure out. There is an expectation that I can do this. There is an expectation that it’s sensible. For fractions, we say three fifths. The Chinese is literally, ‘out of five parts, take three.’ That’s telling you conceptually what a fraction is. It’s differentiating the denominator and the numerator.” The much-storied disenchantment with mathematics among western children starts in the third and fourth grade, and Fuson argues that perhaps a part of that disenchantment is due to the fact that math doesn’t seem to make sense; its linguistic structure is clumsy; its basic rules seem arbitrary and complicated. Asian children, by contrast, don’t face nearly that same sense of bafflement. They can hold more numbers in their head, and do calculations faster, and the way fractions are expressed in their language corresponds exactly to the way a fraction actually is—and maybe that makes them a little more likely to enjoy math, and maybe because they enjoy math a little more they try a little harder and take more math classes and are more willing to do their homework, and on and on, in a kind of virtuous circle. When it comes to math, in other words, Asians have built-in advantage. . ." Here's a link to Gladwell's website which contains the extract. gladwell.com/outliers/rice-paddies-and-math-tests/ Base-10 System Gladwell mainly talks about the words that the Chinese use for numbers and the structure inherent in them, but there is actually another more interesting way we can embed structure in our number system. Our current number system is base-10, which means that we have different symbols for all the numbers up to 10 (0,1,2,3,4,...,9), and then when we get to the number 10, we use the first number again but we move it over one place, and then put a zero in it's place. When we are teaching a child how to write numbers, this is exactly how we explain it to them. For example to write two hundred and seven, we would tell them that they need to put a 2 in the hundreds columns a 0 in the tens column and a 7 in the units column - 207. The fact that we use a base-10 number system is actually just a historical quirk. The only reason humans started to use it is just that we have 10 fingers, there's no particular mathematical benefit to a base-10 system. We could actually base our number system on any integer. The most commonly used alternative is the binary number system used extensively in computing. The binary number system is a base-2 number system where we only have 2 symbols - 0 and 1. The trick is that instead of reusing the first symbol when we get to ten, we do it when we get to two. So the sequence of numbers up to 10 in binary is: In fact we don't even need to restrict ourselves to integers as the base of our number system. For example, we could even use base $ \pi $! Under this system if we want to write $ \pi $, then we would just write 1, to write $ \pi^2 $ it would just be 10. Writing one in base $ \pi $ would be quite difficult though, and we would need to either write $ 1 / {\pi} $ or invent a new character. Base 12 number system So what would be the ideal number on which to base our number system? I'm going to make the argument that a base 12 number system would be the best option. 12 has a large number of small factors and this makes it ideal as a base.
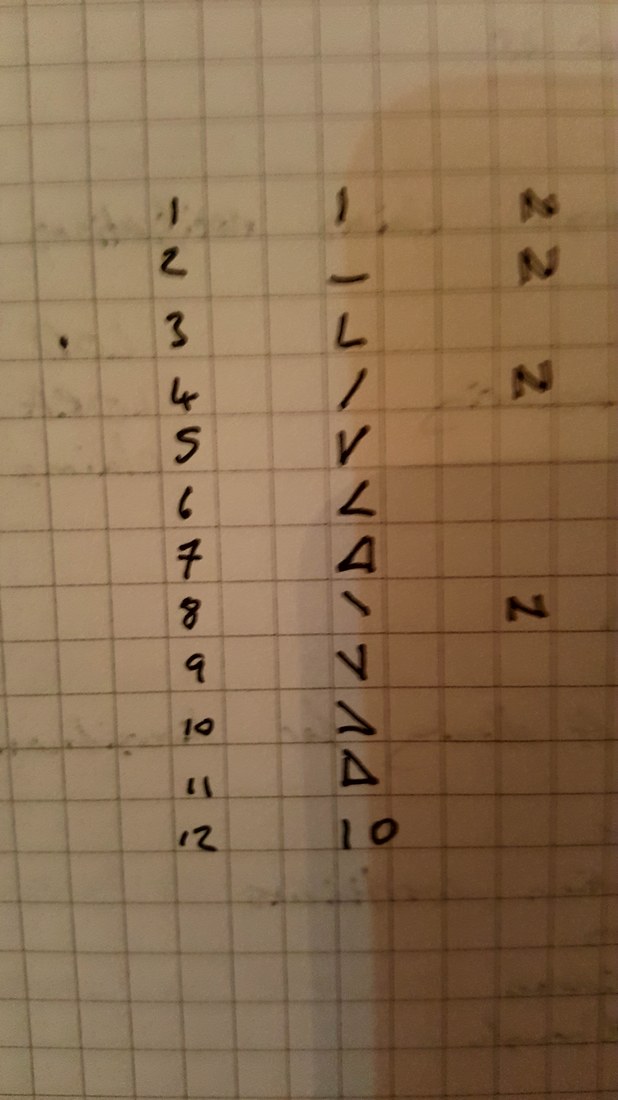
Returning back to Gladwell's idea, another change we could make to the number system to help make it more structured is to change the actual symbols we use for the integers. Here was my attempt from 2011 for alternative symbols we could use. My approach was to embed as much structure into the numbers as possible, so the symbol for three is actually just a combination of the symbols for one and two. This applies for all the numbers other than one, two, four, and eight. I wonder if it would be possible to come up with some sort of rule about how the symbols rotate to further reduce the total number of symbols and also to add some additional structure to the symbols. Let me know if you can think of any additional improvements that could be made to our number system. I think the first time I read about the Difference Engine was actually in the novel of the same name by William Gibson and Bruce Sterling. The book is an alternative history, set in the 19th centuary where Charles Babbage, actually finished building the Difference Engine, a Mechanical calculator he designed. This in turn lead to him getting funding for the Analytical Engine, a Turing-complete mechanical computer which Babbage also designed in real life, but also didn't actually finish building. I really enjoyed the book, but how plausible was this chain of events? How did the Difference Engine work? And what problem was Babbage trying to solve when he came up with the idea for the Difference Engine? Computers before Computers Before electronic computers were invented, scientist and engineers were forced to use various tricks and short cuts to enable them to carry out difficult calculations by hand. One short cut that was used extensively, and one which Babbage would have been very familiar with, was the use of log tables to speed up multiplication. A log tables is simply a table which lists the values of the logarithmic function. If like me you've never used a log table, then how are they useful? Log Tables The property of logarithms that makes them useful in simplifying certain calculations is that: $ log(AB) = log(A) + log(B) $ We use this property often in number theory when we wish to turn a multiplicative problem in to an arithmetic problem and vice versa. In this case it's more straightforward though. If we want to calculate $A*B$ we can convert the figures into logs, and then we just need to add the logs together and convert back to obtain the value of $A*B$. Lets say we want to calculate $ 134.7 * 253.9 $ . What we can do instead is calculate: $ log( 134.7) = 2.1294 $ and $ log (253.9) = 2.4047 $ then we just need to add together $ 2.1294 + 2.4047 = 4.5341 $ and convert back from logs
$ 10^{4.5340} = 34200 $ which we can easily verify as the number we require. Haven't we just made our problem even harder though? Before we needed to multiply two numbers, and now instead we need to do two conversions and an addition, admittedly it's easier to add two large numbers together than multiply them, but what about the conversion? The way around this is to have a book of the values of the log function so that we can just look up the log of any number we are interested in, allowing us to easily convert to and from logs. This is probably a good point to introduce Charles Babbage properly, Babbage was an English Mathematician, Inventor, and Philosopher born in 1791. He was a rather strange guy, as well as making important contributions to Computer Science, Mathematics and Economics, Babbage founded multiple societies. One society was founded to investigate paranormal activity, one was founded to promote the use of Leibniz notation in calculus, and another was founded in an attempt to foster support for the banning of organ grinders. When he wasn't keeping himself busy investigating the supernatural, Babbage was also a keen astronomer. Since astronomy is computation heavy, this meant that Babbage was forced to make extensive use of the log tables that were available at the time. These tables had all been calculated by hand by people called computers. Being a computer was a legitimate job at one point, they would sit and carry out calculations by hand all day every day, not the most exciting job if you ask me. Because the log tables had all been created by teams of human calculators, errors had naturally crept in. The tables were also very expensive to produce. This lead Babbage to conceive of a mechanical machine for calculating log tables, he called this invention the Difference Engine. Method of differences A difference engine uses the method of finite differences to calculate the integer values of polynomial functions. I remember noticing something similar to the method of finite differences when I was playing around trying to guess the formulas for sequences of integers at school. If someone gives you an integer sequence and they ask you to find the formula, say we are given, $1,4,7,10,13,...$ Then, in this case, the answer is easy, we can see that we are just adding 3 each time. To make this completely obvious, we can write in the differences between the numbers.. 1 - 4 - 7 - 10 - 13 - ... 3 3 3 3 What if we are given a slightly more complex sequence though? For example: $1,3,6,10,15,...$ This one is a bit more complicated, let's see what happens when we add in the differences again: 1 - 3 - 6 - 10 - 15 2 3 4 5 Now we see that there is an obvious pattern in the number we are adding on each time. Looking at the differences between these numbers we see: 1 - 3 - 6 - 10 - 15 2 3 4 5 1 1 1 So what's happened here? We now have stability on the second level of the differences. It turns out that this is equivalent to the underlying formula being a quadratic. In this case the formula is $0.5*x^2+1.5x+1$. If we assume the first number in the sequence is equivalent to $x=0$ we can now easily recreate the sequence, and easily calculate the next value. Let's try a difficult example, if we are given the following sequence and told to guess the next value, we can use a similar method to get the answer. $2,5,18,47,98,177$ Setting up the method: 2 - 5 - 18 - 47 - 98 - 177 3 13 29 51 79 10 16 22 28 6 6 6 Since we get a constant at the third level, this sequence must be a cubic, once we know this, it's much easier to guess what the actual formula is. In this case it is x^3-x^2-x+3. Babbage's insight was that we can calculate the next value in this sequence just by adding on another diagonal to this table of differences. Adding $6$ to $28$ gives $34$, then adding $34$ to $79$ gives $113$, and then adding $113$ to $177$ gives us $290$. Which means that the next value in the sequence is $290$ So we get: 2 - 5 - 18 - 47 - 98 - 177 - 290 3 13 29 51 79 113 10 16 22 28 34 6 6 6 6 As you might guess, this process generalises to higher order polynomials. For a given sequence, if we keep trying the differences of the differences and eventually get to a constant then we will know the sequence is formed by a polynomial, and we will also know the degree of the polynomial. So if you are ever a given an integer sequence and asked to find the pattern, always check the differences and see if it eventually becomes a constant, if it does, then you will know the order of the polynomial which defines the sequence and you will also be able to easily compute the next value directly. So how does this apply to Babbage's difference engine? The insight is that we have here a method of enumerating the integer values of a polynomial just using addition. Also at each stage we only need to store the values of the leading diagonal. And each polynomial is uniquely determined by specifying its differences. The underlying message is that multiplication is difficult. In order to come up with a shortcut for multiplication, we use log tables to make the problem additive. And even further, we now have a method for calculating the log function which also avoids multiplication. So given we have this method of calculating the integer values of a polynomial, how can we use this to calculate values of the log function? Approximating Functions The obvious way to approximate a log function with a polynomial would be to just take its Taylor expansion. For example, the Taylor expansion of $ log ( 1 - x ) $ is: $ log ( 1 - x ) = - \sum^{\infty}_{n=1} \frac{x^n}n $ There is a downside to using the Taylor expansion though. Given the mechanical constraints at the time, Babbagge's Difference Engine could only simulate a 7th degree polynomial. So how close can we get with a Taylor expansion? We can use Taylor's theorem to calculate the convergence of the approximation, but this will be quite a bit of work, and since we can easily calculate the actual value of the log function it's easier to just test the approximation with a computer. So taking $log(0.5)$ as an example, when I use a calculator, I am told that it equals $-0.6931$, but when I check the 7th order polynomial I get $-0.6923$, and it's not until I get to the 10th polynomial that we are accurate even to 4 digits. If we require a more accurate approximation, we will have to use numerical methods in conjunction with a restriction on the range of convergence. This would mean that if we wished to compute $log(x)$ on the interval [0,1], for 100 different points on the interval, we would break [0,1] into sub-intervals and then use a different polynomial fit for each sub-interval. If you'd like to read more about how the actual machine worked then the Wikipedia is really useful. en.wikipedia.org/wiki/Difference_engine And if you are interested in reading more about the mathematics behind using a Difference Engine then the following website is really good: ed-thelen.org/bab/bab-intro.html |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
 RSS Feed
RSS Feed