Here is an Acronym I came up with for remembering the reasons for setting up a captive Insurance company:

Claims control
Access to Reinsurance
Profit loading and Acquisition costs
Tax and Regulatory optimization
Investment income
Volatility in premium rates
Extension of coverage

Claims control - As the captive is directly controlled by the parent company, the parent company is free to establish the claims handling procedures. For example, they may wish the captive to operate a very liberal interpretation of what is covered under the policy, thereby reducing the possibility that the parent company will be exposed to a financial loss which they thought they were indemnified from. If the parent company were dealing with a commercial insurer instead then they would be at the mercy of the exact policy wording.

Access to Reinsurance - By self insuring, the parent company gives itself the option of then ceding the risk directly to a reinsurer rather than going through an insurance company. Reinsurers tend to enjoy greater economies of scale than direct writers, and incur lower acquisition and claims handling costs due to the smaller number of clients they deal with. Therefore the premiums charged by a reinsurer would be lower than that charged by a direct writer.

Profit loading and acquisition costs – Due to the fact that most insurers are run as limited liability companies, the premiums that are charged by the insurer will be loaded for profit. There will also be significant loadings for expenses and acquisition costs (the costs associated with acquiring new business). By setting up a captive the parent company can eliminate these loadings and instead just pay a pure risk premium. These loadings can be significant, sometimes as high as 50%.

Investment Income – The captive will be required to hold capital to cover the liabilities that it is taking on by accepting the risk from the parent company. This capital can be invested and the investment income retained in the captive. This investment income would otherwise be earned by the insurance company. (Admittedly the insurance company would be expected to reflect this fact in the premium that it charges however this may not always be the case)

Volatility in premiums rates - If the parent company uses a commercial insurer rather than a captive then the premium charged by the insurance company will be partly market driven. Premium rates vary over time in line with the underwriting cycle beyond how they would be expected to vary based on the pure risk premium. The underwriting cycle is related to the cost of capital and the level of profit and competition between insurance companies. This can add an additional level of volatility to the premiums paid by the parent company. By setting up a captive the parent company can help stabilize the premiums that it pays.
 
Extend coverage – Insurers may be unwilling to accept certain risks which they deem to large or too unique, or they may charge premiums that are excessively cautious when taking on these risks. The ability to dictate to a captive the risks that it should accept extends the coverage available to the parent company. This is one of the primary reasons for setting up a captive.


 

Part 3 consists of four questions. The answer to each puzzle is a single word, which can be used to create a URL."
​

1. Complete the sequence:
   Buck, Cod, Dahlia, Rook, Cuckoo, Rail, Haddock, ?

My first thought when reading this was to look at the semantic meaning. I think this is probably because of the fact that we have both cod and haddock in the list, and quite a few of the others are animals. After playing around with this for a while I was getting nowhere. Then I noticed that the entire sequence of letters is nearly a palindrome. Therefore, the answer is cub, as this turns the sequence into a palindrome.


     2. Sum:
         pest + √(unfixed - riots) = ? 

Hmm, how can we do maths with words? I played around with trying to assign meaning to the sentence, kinda like the old joke that you can show that $women = evil$.

Women take up time and money, therefore:

$Women = Time * Money$

Time is equal to money:

$Time = Money$

Therefore:

$Women = Money^2$

But we also know that money is the root of all evil:

$Money = \sqrt{Evil}$

Therefore:

$Women = \sqrt{{Evil}^2}$

Simplifying:

$Women = Evil$
​
I wasn't able to come up with anything along this vein, therefore we need to try a new approach.

If we are committing to the idea that the words represent numbers somehow then we need to try to assign numbers to these words. I played around with a few ideas before trying anagrams.

I noticed that pest is an anagram of sept. (Which I initially thought related to September and hence 9, but is also French for 7). Running with this idea, we also note that unfixed is an anagram for dix-neuf, and riots is an anagram for trois. So our equation becomes:

$ 7 + \sqrt{19 - 3} = 7 + \sqrt{16} = 7 + 4 = 11$

Therefore our answer is onze. Since the other words were anagrams this is probably an anagram as well. Therefore I think the solution is zone. On to the next question.

     3. Samuel says: if agony is the opposite of denial, and witty is the opposite of tepid, then      what is the opposite of smart?

Samuel says is a strange way to start this question. normally you'd say 'simon says', is this a hint? Who is Samuel? The first thing that comes to my mind is Samuel Pepys, the famous diarist. I wonder if he has any famous quotes that shed light on the question. A quick google doesn't reveal anything. Perhaps this is a different Samuel? Looking up other famous Samuels leads us to another clue - Samuel Morse. Once we know that we are talking about morse code, the obvious next step is to convert the words we've been given into morse code. We find that:
Agony = ... -- .- .-. -
Denial = -.. . -. .. .- .-..
Witty = .-- .. - - -.--
Tepid = - . .--. .. -..
Smart = ... -- .- .-. -

Now we can hopefully see how this works - we replace the dots for dashes.

Therefore our new word is:
​---..-.-.-.-

This word doesn't have the spaces in it. After some experimentation we conclude that the word that is the opposite of smart is often.

     4. The answers to the following cryptic crossword clues are all words of the same      length. We have provided the first four clues only. What is the seventh and last answer? 
 

1. Withdraw as sailors hold festive sing-song
2. It receives a worker and returns a queen
3. Try and sing medley of violin parts
4. Fit for capture
   
   
   
5. ?

The next question is a series of cryptic crosswords - which is a bit of an issue since I've never done a cryptic crossword before. We've therefore got two options - learn how to solve cryptic crosswords, or find another way to progress. I attempted to learn how to do cryptic crosswords but I really struggled to solve the crosswords here, though I do now know how to solve cryptic crosswords and can solve a few questions in a newspaper. Therefore we need to find another way to solve this puzzle.

The website provides us with a way to check that our answers are correct. We can input our answers into the boxes provided and click the 'check answer' button and the website will tell us if we have the correct solutions. Hmm.. wonder how this words.

When we view page source and look at the code we see that there is actually a check function. For a given string of letters this function returns two unique numbers. The website takes our answers, calculates the unique numbers associated with it, and checks if the numbers generated are equal to 608334672 and 46009587. So it's simple right? We just work out the string generates these two numbers and this will give us the answer. The problem with this is that the function that generates these numbers is something called a cryptographic hash function. Which is a function which for any input will return a result of a fixed length which is practically impossible to invert.

We have some extra information that help us though - we know the format of the answer, and we know the answers to three out of the four questions. So we know the input to the hash function is of the form:
"cubzoneoften" + new word

I therefore set up a dictionary attack in the following file:

This file works by letting you open a .txt file containing a list of words. The code will then loop through the words in the text file, calculating the results of the hash function. After running this file we find out that the word we are looking for is layered. And the url of the next stage of the challange is:
​

 In Options, Futures and Other Derivatives, Chapter 10, Hull derives lower bounds for option prices for European put and call options for dividend paying stocks.

The result in Hull:

For a call option:

​For a put option:

And he also derives upper bounds for European put and call options for non-dividend paying stocks.

For a call option:

​For a put option:

​But he doesn't derive upper bounds for European put and call options for dividend paying stocks. And for call options this gives us a tighter upper bound. Also I wasn't able to find this bound online for some reason, it's almost like everyone is just copying these results from other people and not actually deriving them themselves.

The new Result

As we saw in my post on part 1 of the GCHQ Christmas puzzle, the solution to the grid puzzle gives us a QR code which takes us to the following website:

Part 2 of the puzzle states:

"Part 2 consists of six multiple choice questions. You must answer them all correctly before you can move on to Part 3."

We are then given our first question:

Q1. Which of these is not the odd one out?

1. STARLET
2. SONNET
3. SAFFRON
4. SHALLOT
5. TORRENT
6. SUGGEST

This is a strangely worded question... which of these is not the odd one out. We are more used to being asked which of these is the odd one out. What would it mean for something not to be the odd one out? My initial reading of the question, which turned out to be the correct one, is that each word except for one will turn out to be the odd one out for a different reason. For example, TORRENT is the only not starting with an S, therefore, it is the odd one out, and not the answer to the puzzle. SAFFRON is the only on ending in an N and is also there not the answer to the puzzle.

As an aside, this question reminds me of the interesting number paradox. If we attempt to divide all numbers up into numbers that are interesting (such as 2 which is the only even prime) and numbers which are not interesting. Then the numbers that are not interesting must have a smallest member. However, since this is an interesting property (the property of being the smallest uninteresting number), this number cannot in fact be an uninteresting number. And we must conclude that there are no uninteresting number. Similarly, if we work out that one of the answers above is not the odd one out, then we have found a way in which the number is the odd one out. Due to the fact that it is the only one which is not the odd one out! 

Q2. What comes after GREEN, RED, BROWN, RED, BLUE, -, YELLOW, PINK?

1. RED
2. YELLOW
3. GREEN
4. BROWN
5. BLUE
6. PINK

This turns out to be a cool question. We have a sequence of colours and we need to work out the next value. My first thought when I read this was that it perhaps relates to monopoly (possibly because I had played it just before trying to answer). I played around with this idea for a while but didn't get anywhere. I wasn't a million miles away as in the end my girlfriend gave me a hint that it related to snooker. Once you plug in the values of the snooker balls into this sequence you get the following sequence of numbers:

3   1   4   1   5   -   2   6

Which you will hopefully recognise as the decimal expansion of $\pi$. The next digit is 5 and therefore the answer is Blue.

Q3. Which is the odd one out?

1. MATURE
2. LOVE
3. WILDE
4. BUCKET
5. BECKHAM
6. SHAKA

I had no idea how to solve this question. I tried googling all the names but couldn't really see any common links. Below I show how to progress even though you haven't answered all the questions.

Q4. I was looking at a man on top of a hill using flag semaphore to send a message, but to me it looked like a very odd message. It began "ZGJJQ EZRXM" before seemingly ending with a hashtag. Which hashtag?

1. #SGM
2. #SEM
3. #SEN
4. #SGN
5. #TEN
6. #TGN

​
This should be quite a straightforward question to answer - my guess which turned out to be correct is that there is a fairly straight forward transformation that can be applied to how the man is using flag semaphore so that it makes sense. The first transformation I tried was to rotate the message by various degrees. I got bored of answering this question after a while so I decided to skip it. .

Q5. What comes after 74, 105, 110, 103, 108, 101, 98, 101, 108, 108?

1. 108
2. 101
3. 115
4. 123
5. 111
6. 103

Here we have a sequence of numbers and we need to find the next number. Since the number all cluster around the 70-110 area, my intuition was that they are some sort of encoding. The first thing I checked was the ascii values of these numbers. They come out as J i n g l e b e l l. This should be the answer then! The next value is s, and the next number is therefore 115.

Ascii is a way for computers to represent letters and other characters using numbers. The numbers 0 to 255 (giving a total of 256 characters which is a power of 2) are each assigned a character here is a link to an ascii table:

Q6. What comes next: D, D, P, V, C, C, D, ?

1. F
2. E
3. D
4. C
5. B
6. A

This was quite a fun question. I've got no idea how to help people solve it as I just stared at it for a few minutes then spotted the answer. These are the names of Santa's reindeers! I guess one possible hint was the use of jinglebells in the question above, and the fact that this is a Christmas puzzle.

So we have the answer to 3 of the questions and we have narrowed down some of the options on the other questions.

I noticed that the way the website stores your responses is to take the 6 answers and convert it to a web address. So by answering 1 on each question we will be taken to the following url. (Note the 6 As at the end which correspond to answering 1 in each question)

What I did next was set up a Spreadsheet with links to this url corresponding to the possible combinations of answers which I have not eliminated yet. For example, we know that the second digit is E and the second to last digit is C. The url of the next stage is the following:

I was working through Hull's Options, Futures and other Derivatives when Hull states that the price of a Bond paying semi annual coupons in line with six month LIBOR, and discounted using a six month LIBOR discount rate is par. To me this statement seems like it's probably true but I wasn't 100%. I couldn't find the proof online, but it turns out that it is true, here is my derivation.

When you order at 5 guys burgers (which you should if you haven't because they are amazing) you are given a ticket between 1 and 100 which is then use to collect your order. Last time I was there my friend suggested trying to collect all 100 tickets. The question is:

Assuming you receive a random ticket number between 1 and 100 inclusive on every visit. On average, how many visits would it take to collect all 100 tickets?

Solution:

To help us analyse $S$ we need to define another collection of random variables.

Let $X_i$ denote the number of purchases required to get the $ith + 1$ ticket given we have already collected $i$ tickets. So if we have collected 2 tickets (say ticket number 33 and ticket number 51) and the next two tickets we get are 33 and 81, then $X_2 = 2$ because it took us 2 attempts to get a new unique ticket.

We can actually view $S$ as the sum of these $X_i$, i.e. $S = \sum\limits_{i=1}^{100}X_i$ (to see that this is the case the number of visit it takes to collect all 100 tickets will be the number of visits to collect the first ticket plus the number of visits to collect the 2nd unique ticket, and so on)

There are two further observations that we need to make before deriving the solution. Firstly, each $X_i$ is independent of $\sum\limits_{k=1}^{{i-1}}X_i$. Secondly, each $X_i$ is actually distributed as a Geometric Distribution where:

This year GCHQ released a Christmas Puzzle, in this post I'll show you how to solve the series of puzzles, and also, the thought process that I used to get to the solutions.

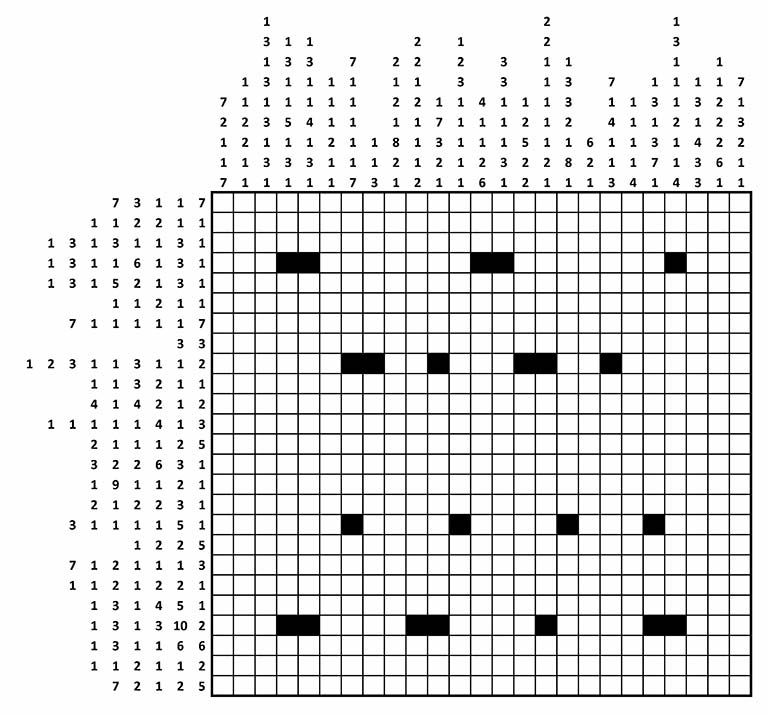
If you would like to attempt to solve the puzzle yourself then here is the link to the first part of the puzzle. The solution to the first part will then lead to the second part of the puzzle. In total there are five parts.

From the GCHQ website:

"In this type of grid-shading puzzle, each square is either black or white. Some of the black squares have already been filled in for you.

Each row or column is labelled with a string of numbers. The numbers indicate the length of all consecutive runs of black squares, and are displayed in the order that the runs appear in that line. For example, a label "2 1 6" indicates sets of two, one and six black squares, each of which will have at least one white square separating them."

I decided to solve this puzzle in excel. The main reason for this was that I wanted to be able to fill in squares automatically rather than shading them by hand. I've posted a link to an excel file below which matches the start of the puzzle. In my version if you press Ctrl+a then the selected cell will turn black, and if you press ctrl+d then the selected cell will turn blue. I'll explain the use of blue cells later.

 The first step to solving this puzzle is to count the number of rows and columns in the grid. In this case we have a 25 by 25 grid. In excel I then calculated the minimum number of cells required for each row and column. For example, the third column is listed as 1,3,1,3,1,3,1,3,1. Since there must be a blank space in between each block of black cells, this combination must take up a minimum of 25 cells but since there are only 25 cells in the column we now know which cells in this column need to be coloured black. We can now go ahead and fill in this column. We also know that the spaces in between the blocks of black cells need to be blank, to signify this we can colour these cells blue. Repeating this process allows us to complete 3 columns and 2 rows.

The next step is to look at rows and columns which have high minimum values but which are less than 25 but still high. For example, looking at the first row, it is listed as 7,3,1,1,7 with a minimum of 23. Since the first two blocks on either side are 7 long, cells 17:23 must be coloured in as a minimum, but as a maximum cells 19:25 must be filled in. Since there is an overlap between these two we can colour in the cells in the overlap. Here is an image demonstrating this. There are three copies of the first row, the first row contains the minimum cells and the second row contains the maximum cells. I have then coloured the overlap on the blocks of seven in black.

Filling in the first cell in a row is also useful as it lets us immediately use the information about that column. For example we know that the third cell in the first row is black, looking at the listing for this column we see that the first block of blacks is a 1, therefore the cell below it in the second column must be blank and can be filled in blue. Using this these techniques we eventually complete the grid. Giving the following image.

You may recognise this kind of pattern as a QR code. A QR Code is a 2 dimensional bar code. I downloaded a QR reader to my phone and scanned the image which takes you to the following url: