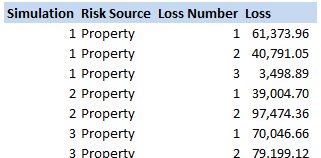
Compound Poisson Loss Model in VBA13/12/2017 I was attempting to set up a Loss Model in VBA at work yesterday. The model was a Compound-Poisson Frequency-Severity model, where the number of events is simulated from a Poisson distribution, and the Severity of events is simulated from a Severity curve. There are a couple of issues you naturally come across when writing this kind of model in VBA. Firstly, the inbuilt array methods are pretty useless, in particular dynamically resizing an array is not easy, and therefore when initialising each array it's easier to come up with an upper bound on the size of the array at the beginning of the program and then not have to amend the array size later on. Secondly, Excel has quite a low memory limit compared to the total available memory. This is made worse by the fact that we are still using 32-bit Office on most of our computers (for compatibility reasons) which has even lower limits. This memory limit is the reason we've all seen the annoying 'Out of Memory' error, forcing you to close Excel completely and reopen it in order to run a macro. The output of the VBA model was going to be a YLT (Yearly Loss Table), which could then easily be pasted into another model. Here is an example of a YLT with some made up numbers to give you an idea: It is much quicker in VBA to create the entire YLT in VBA and then paste it to Excel at the end, rather than pasting one row at a time to Excel. Especially since we would normally run between 10,000 and 50,000 simulations when carrying out a Monte Carlo Simulation. We therefore need to create and store an array when running the program with enough rows for the total number of losses across all simulations, but we won't know how many losses we will have until we actually simulate them. And this is where we come across our main problem. We need to come up with an upper bound for the size of this array due to the issues with dynamically resizing arrays, but since this is going to be a massive array, we want the upper bound to be as small as possible so as to reduce the chance of a memory overflow error. Upper Bound What we need then is an upper bound on the total number of losses across all the simulations years. Let us denote our Frequency Distribution by $N_i$, and the number of Simulations by $n$. We know that $N_i$ ~ $ Poi( \lambda ) \: \forall i$. Lets denote the total size of the YLT array by $T$. We know that $T$ is going to be: $$T = \sum_{1}^{n} N_i$$ We now use the result that the sum of two independent Poisson distributions is also a Poisson distribution with parameter equal to the sum of the two parameters. That is, if $X$ ~ $Poi( \lambda)$ , and $Y$ ~ $Poi( \mu)$, then $X + Y$ ~ $Poi( \lambda + \mu)$. By induction this result can then be extended to any finite sum of independent Poisson Distributions. Allowing us to rewrite $T$ as: $$ T \sim Poi( n \lambda ) $$ We now use another result, a Poisson Distribution approaches a Normally Distribution as $ \lambda \to \infty $. In this case, $ n \lambda $ is certainly large, as $n$ is going to be set to be at least $10,000$. We can therefore say that: $$ T \sim N ( n \lambda , n \lambda ) $$ Remember that $T$ is the distribution of the total number of losses in the YLT, and that we are interested in coming up with an upper bound for $T$. Let's say we are willing to accept a probabilistic upper bound. If our upper bound works 1 in 1,000,000 times, then we are happy to base our program on it. If this were the case, even if we had a team of 20 people, running the program 10 times a day each, the probability of the program failing even once in an entire year is only 4%. I then calculated the $Z$ values for a range of probabilities, where $Z$ is the unit Normal Distribution, in particular, I included the 1 in 1,000,000 Z value. We then need to convert our requirement on $T$ to an equivalent requirement on $Z$. $$ P ( T \leq x ) = p $$ If we now adjust $T$ so that it can be replaced with a standard Normal Distribution, we get: $$P \left( \frac {T - n \lambda} { \sqrt{ n \lambda } } \leq \frac {x - n \lambda} { \sqrt{ n \lambda } } \right) = p $$
Now replacing the left hand side with $Z$ gives:
$$P \left( Z \leq \frac {x - n \lambda} { \sqrt{ n \lambda } } \right) = p $$
Hence, our upper bound is given by:
$$T \lessapprox Z \sqrt{n \lambda} + n \lambda $$
Dividing through by $n \lambda $ converts this to an upper bound on the factor above the mean of the distribution. Giving us the following:
$$ T \lessapprox Z \frac {1} { \sqrt{n \lambda}} + 1 $$
We can see that given $n \lambda$ is expected to be very large and the $Z$ values relatively modest, this bound is actually very tight.
For example, if we assume that $n = 50,000$, and $\lambda = 3$, then we have the following bounds: So we see that even at the 1 in 1,000,000 level, we only need to set the YLT array size to be 1.2% above the mean in order to not have any overflow errors on our array. References (1) Proof that the sum of two independent Poisson Distributions is another Poisson Distribution math.stackexchange.com/questions/221078/poisson-distribution-of-sum-of-two-random-independent-variables-x-y
(2) Normal Approximation to the Poisson Distribution.
stats.stackexchange.com/questions/83283/normal-approximation-to-the-poisson-distribution |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
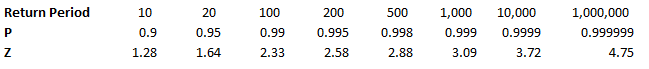
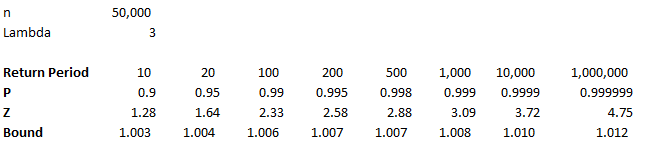
 RSS Feed
RSS Feed
Leave a Reply.