Correlation Matrix - Positive Semi-Definite Requirement

If you have played around with Correlating Random Variables using a Correlation Matrix in  [insert your favourite financial modelling software] then you may have noticed the requirement that the Correlation Matrix be positive semi-definite.

But what exactly does this mean? And how would we check this ourselves in VBA or R?

Mathematical Definition​

Let's start with the Mathematical definition. To be honest, it didn't really help me much in understanding what's going on, but it's still useful to know.
​

A symmetric $n$ x $n$ matrix $M$ is said to be positive semidefinite if the scalar $z^T M z $ is positive for every non-zero column vector $z$ of $n$ real numbers.

If I am remembering my first year Linear Algebra course correctly, then Matrices can be thought of as transformations on Vector Spaces. Here the Vector Space would be a collection of Random Variables. I'm sure there's some clever way in which this gives us some kind of non-degenerate behaviour. After a bit of research online I couldn't really find much.

Intuitive Definition

The intuitive explanation is much easier to understand. The requirement comes down to the need for internal consistency between the correlations of the Random Variables.

For example, suppose we have three Random Variables, A, B, C.

Let's suppose that A and  B are highly correlated, that is to say, when A is a high value, B is also likely to be a high value. Let's also suppose that A and C are highly correlated, so that if A is a high value, then C is also likely to be a high value. We have now implicitly defined a constraint on the correlation between B and C. If A is high both B and C are also high, so it can't be the case that B and C are negatively correlated, i.e. that when B is high, C is low.

Therefore some correlation matrices will give relations which are impossible to model.

Alternative characterisations

You can find a number of necessary and sufficient conditions for a matrix to be positive definite, I've included some of them below. I used number 2 in the VBA code for a real model I set up to check for positive definiteness.

1. All Eigenvalues are positive. 

If you have studied some Linear Algebra, then you may not be surprised to learn that there is a characterization using Eigenvalues. It seems like just about anything to do with Matrices can be restated in terms of Eigenvalues. I'm not really sure how to interpret this condition though in an intuitive way.

2. All leading principal minors are all positive

This is the method I used to code the VBA algorithm below. The principal minors are just another name for the determinant of the upper-left $k$ by $k$ sub-matrix. Since VBA has a built in method for returning the determinant of a matrix this was quite an easy method to code.

3. It has a unique Cholesky decomposition

I don't really understand this one properly, however I remember reading that Cholesky decomposition is used in the Copula Method when sampling Random Variables, therefore I suspect that this characterisation may be important!

Since I couldn't really write much about Cholesky decomposition here is a picture of Cholesky instead, looking quite dapper.

​All 2x2 matrices are positive semi-definite

Since we are dealing with Correlation Matrices, rather than arbitrary Matrices, we can actually show a-priori that all 2 x 2 Matrices are positive semi-definite.

Proof

Let M be a $2$ x $2$ correlation matrix.

$$M = \begin{bmatrix} 1&a\\ a&1 \end{bmatrix}$$

And let $z$ be the column vector $M = \begin{bmatrix} z_1\\ z_2 \end{bmatrix}$

Then we can calculate $z^T M z$

$$z^T M z = {\begin{bmatrix} z_1\\ z_2 \end{bmatrix}}^T \begin{bmatrix} 1&a\\ a&1 \end{bmatrix} \begin{bmatrix} z_1\\ z_2 \end{bmatrix} $$

Multiplying this out gives us:

$$ = {\begin{bmatrix} z_1\\ z_2 \end{bmatrix}}^T \begin{bmatrix} z_1 & a z_2 \\ a z_1 & z_2 \end{bmatrix} = z_1 (z_1 + a z_2) + z_2 (a z_1 + z_2)$$

We can then simplify this to get:

$$ = {z_1}^2 + a z_1 z_2 + a z_1 z_2 + {z_2}^2 = (z_1 + a z_2)^2 \geq 0$$

​Which gives us the required result. This result is consistent with our intuitive explanation above, we need our Correlation Matrix to be positive semidefinite so that the correlations between any three random variables are internally consistent. Obviously, if we only have two random variables, then this is trivially true, so we can define any correlation between two random variables that we like.

Not all 3x3 matrices are positive semi-definite

The 3x3 case, is simple enough that we can derive explicit conditions. We do this using the second characterisation, that all principal minors must be greater than or equal to 0.

Demonstration

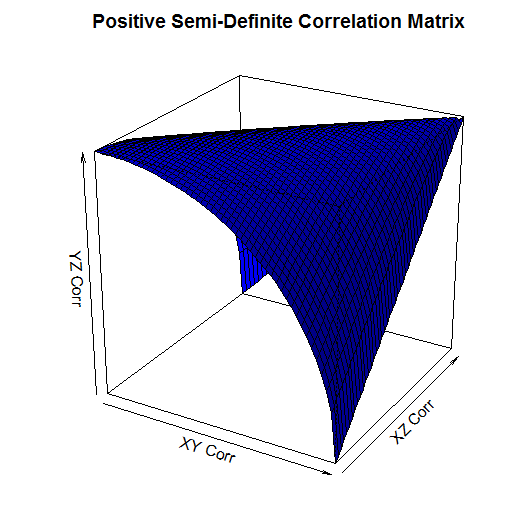
Let M be a $3$ x $3$ correlation matrix:

$$M = \begin{bmatrix} 1&a&b\\ a&1&c \\ b&c&1 \end{bmatrix}$$

We first check the determinant of the $2$ x $2$ sub matrix. We need that:

$ \begin{vmatrix} 1 & a \\ a & 1 \end{vmatrix} \geq 0 $

By definition:

$ \begin{vmatrix} 1 & a \\ a & 1 \end{vmatrix} = 1 - a^2$

We have that $ | a | \leq 1 $, hence $ | a^2 | \leq 1 $, and therefore:

$ | 1- a^2 | \geq 0 $

Therefore the determinant of the $2$ x $2$ principal sub-matrix is always positive.

Now to check the full $3$ x $3$. We require:

$ \begin{vmatrix} 1 & a & b \\ a & 1 & c \\ b & c & 1 \end{vmatrix} \geq 0 $

By definition:

$ \begin{vmatrix} 1 & a & b \\ a & 1 & c \\ b & c & 1 \end{vmatrix} = 1 ( 1 - c^2) - a (a - bc) + b(ac - b) = 1 + 2abc - a^2 - b^2 - c^2 $

Therefore in order for a $3$ x $3$ matrix to be positive demi-definite we require:

$a^2 + b^2 + c^2 - 2abc = 1 $

I created a 3d plot in R of this condition over the range [0,1].
​

​
It's a little hard to see, but the way to read this graph is that the YZ Correlation can take any value below the surface. So for example, when the XY Corr is 1, and the XZ Corr is 0, the YZ Corr has to be 0. When the XY Corr is 0 on the other hand, and XZ Corr is also 0, then the YZ Corr can be any value between 0 and 1.

Checking that a Matrix is positive semi-definite using VBA

When I needed to code a check for positive-definiteness in VBA I couldn't find anything online, so I had to write my own code. It makes use of the excel determinant function, and the second characterization mentioned above. Note that we only need to start with the 3x3 sub matrix as we know from above that all 1x1 and all 2x2 determinants are positive.

This is not a very efficient algorithm, but it works and it's quite easy to follow. 

Function CheckCorrMatrixPositiveDefinite()

Dim vMatrixRange As Variant
Dim vSubMatrix As Variant
Dim iSubMatrixSize As Integer
Dim iRow As Integer
Dim iCol As Integer
Dim bIsPositiveDefinite As Boolean

bIsPositiveDefinite = True


vMatrixRange = Range(Range("StartCorr"), Range("StartCorr").Offset(inumberofrisksources - 1, inumberofrisksources - 1))

' Only need to check matrices greater than size 2 as determinant always greater than 0 when less than or equal to size 2'

If iNumberOfRiskSources > 2 Then
    For iSubMatrixSize = iNumberOfRiskSources To 3 Step -1
        ReDim vSubMatrix(iSubMatrixSize - 1, iSubMatrixSize - 1)
        For iRow = 1 To iSubMatrixSize
            For iCol = 1 To iSubMatrixSize
                vSubMatrix(iRow - 1, iCol - 1) = vMatrixRange(iRow, iCol)
            Next
        Next
        'If the determinant of the matrix is 0, then the matrix is semi-positive definite'
        If Application.WorksheetFunction.MDeterm(vSubMatrix) < 0 Then
            CheckCorrMatrixisPositiveDefinite = False
            bIsPositiveDefinite = False
        End If
    Next
End If

If bIsPositiveDefinite = True Then
    CheckCorrMatrixPositiveDefinite = True
Else
    CheckCorrMatrixPositiveDefinite = False
End If

End Function



​

Checking that a Matrix is positive semi-definite in R

Let's suppose that instead of VBA you were using an actually user friendly language like R. What does the code look like then to check that a matrix is positive semi-definite? All we need to do is install a package called 'Matrixcalc', and then we can use the following code:

is.positive.definite( Matrix )

That's right, we needed to code up our own algorithm in VBA, whereas with R we can do the whole thing in one line using a built in function! It goes to show that the choice of language can massively effect how easy a task is.