Excel Protect Sheet Encryption27/12/2019
The original idea for this post came from a slight quirk I noticed in some VBA code I was running (code pasted below) If you've ever needed to remove the protect sheet from a Spreadsheet without knowing the password, then you probably recognise it.
Sub RemovePassword() Dim i As Integer, j As Integer, k As Integer Dim l As Integer, m As Integer, n As Integer Dim i1 As Integer, i2 As Integer, i3 As Integer Dim i4 As Integer, i5 As Integer, i6 As Integer On Error Resume Next For i = 65 To 66: For j = 65 To 66: For k = 65 To 66 For l = 65 To 66: For m = 65 To 66: For i1 = 65 To 66 For i2 = 65 To 66: For i3 = 65 To 66: For i4 = 65 To 66 For i5 = 65 To 66: For i6 = 65 To 66: For n = 32 To 126 ActiveSheet.Unprotect Chr(i) & Chr(j) & Chr(k) & _ Chr(l) & Chr(m) & Chr(i1) & Chr(i2) & Chr(i3) & _ Chr(i4) & Chr(i5) & Chr(i6) & Chr(n) If ActiveSheet.ProtectContents = False Then MsgBox "Password is " & Chr(i) & Chr(j) & _ Chr(k) & Chr(l) & Chr(m) & Chr(i1) & Chr(i2) & _ Chr(i3) & Chr(i4) & Chr(i5) & Chr(i6) & Chr(n) Exit Sub End If Next: Next: Next: Next: Next: Next Next: Next: Next: Next: Next: Next End Sub Nothing too interesting so far, the code looks quite straight forward - we've got a big set of nested loops which appear to test all possible passwords, and will eventually brute force the password - if you've ever tried it you'll know it works pretty well. The interesting part is not so much the code itself, as the answer the code gives - the password which unlocks the sheet is normally something like ‘AAABAABA@1’. I’ve used this code quite a few times over the years, and always with similar results, the password always looks like some variation of this string. This got me thinking - surely it is unlikely that all the Spreadsheets I’ve been unlocking have had passwords of this form? So what’s going on? After a bit of research, it turns out Excel doesn’t actually store the original password, instead it stores a 4-digit hash of the password. Then to unlock the Spreadsheet, Excel hashes the password attempt and compares it to the stored hashed password. Since the size of all possible passwords is huge (full calculations below), and the size of all possible hashes is much smaller, we end up with a high probability of collisions between password attempts, meaning multiple passwords can open a given Spreadsheet. I think the main reason Microsoft uses a hash function in this way rather than just storing the unhashed password is that the hash is stored by Excel as an unencrypted string within a xml file. In fact, an .xlsx file is basically just a zip containing a number of xml files. If Excel didn't first hash the password then you could simply unzip Excel file, find the relevant xml file and read the password from any text editor. With the encryption Excel selected, the best you can do is open the xml file and read the hash of the password, which does not help with getting back to the password due to the nature of the hash function. What hash function is used? I couldn't find the name of the hash anywhere, but the following website has the fullest description I could find of the actual algorithm. As an aside, I miss the days when the internet was made up of websites like this – weird, individually curated, static HTML, obviously written by someone with deep expertise, no ads as well! Here’s the link: http://chicago.sourceforge.net/devel/docs/excel/encrypt.html And the process is as follows:
Here is the algorithm to create the hash value:
a -> 0x61 << 1 == 0x00C2 b -> 0x62 << 2 == 0x0188 c -> 0x63 << 3 == 0x0318 d -> 0x64 << 4 == 0x0640 e -> 0x65 << 5 == 0x0CA0 f -> 0x66 << 6 == 0x1980 g -> 0x67 << 7 == 0x3380 h -> 0x68 << 8 == 0x6800 i -> 0x69 << 9 == 0x5201 (unrotated: 0xD200) j -> 0x6A << 10 == 0x2803 (unrotated: 0x1A800) count: 0x000A constant: 0xCE4B result: 0xFEF1 This value occurs in the PASSWORD record.
How many trials will we need to decrypt?
Now we know how the algorithm works, can we come up with a probabilistic bound on the number of trials we would need to check in order to be almost certain to get a collision when carrying out a brute force attack (as per the VBA code above)?
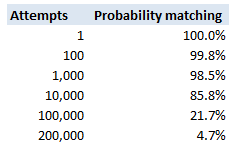
This is a fairly straight forward calculation – the probability of guessing incorrectly for a random attempt is $\frac{1}{65536}$. To keep the maths simple, if we assume independence of attempts, the probability of not getting the password after $n$ attempts is simply: $$ \left( \frac{1}{65536} \right)^n$$ The following table then displays these probabilities
So we see that with 200,000 trials, there is a less than 5% chance of not having found a match.
We can also derive the answer directly, we are interested in the following probabilistic inequality: $$ \left( 1- \frac{1}{65536} \right)^k < 0.05$$ Taking logs of both sides gives us: $$ln \left( 1- \frac{1}{65536}\right)^k = ln( 0.05)$$ And then bringing down the k: $$k * ln \left( 1- \frac{1}{65536} \right) = ln(0.05)$$ And then solving for $k$: $$k = \frac{ ln(0.05)}{ln \left(1- \frac{1}{65536}\right)} = 196,327$$
Can I work backwards to find the password from a given hash?
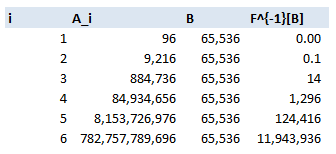
As we explained above, in order to decrypt the sheet, you don’t need to find the password, you only need to find a password. Let’s suppose however, for some reason we particularly wanted to find the password which was used, is there any other method to work backwards? I can only think of two basic approaches: Option 1 – find an inversion of the hashing algorithm. Since this algorithm has been around for decades, and is designed to be difficult to reverse, and so far has not been broken, this is a bit of a non-starter. Let me know if you manage it though! Option 2 – Brute force it. This is basically your only chance, but let’s run some maths on how difficult this problem is. There are $94$ possible characters (A-Z, a-z,0-9), and in Excel 2010, the maximum password length is $255$, so in all there are, $94^{255}$ possible passwords. Unfortunately for us, that is more than the total number of atoms in the universe $(10^{78})$. If we could check $1000$ passwords per second, then it would take far longer than the current age of the universe to find the correct one. Okay, so that’s not going to work, but can we make the process more efficient? Let’s restrict ourselves to looking at passwords of a known length. Suppose we know the password is only a single character, in that case we simply need to check $94$ possible passwords, one of which should unlock the sheet, hence giving us our password. In order to extend this reasoning to passwords of arbitrary but known length, let’s think of the hashing algorithm as a function and consider its domain and range: Let’s call our hashing algorithm $F$, the set of all passwords of length $i$, $A_i$, and the set of all possible password hashes $B$. Then we have a function: $$ F: A_i -> B$$ Now if we assume the algorithm is approximately equally spread over all the possible values of $B$, then we can use the size of $B$ to calculate the size of the kernel $F^{-1}[A_i]$. The size of $B$ doesn’t change. Since we have a $4$ digit hexadecimal, it is of size $16^4$, and since we know the size of $A_i$ is $96$, we can then estimate the size of the kernel. Let’s take $i=4$, and work it through:
$A_4$ is size $96^4 = 85m$, $B = 65536$, hence $|F^{-1}[A_4]| = \frac{85m}{65536} = 124416$
Which means for every hash, there are $124,416$ possible $4$ digit passwords which can create this hash, and therefore may have been the original password. Here is a table of the values for $I = 1$ to $6$:
In fact we can come up with a formula for size of the kernel: $$\frac{96^i}{16^4} \sim 13.5 * 96^{i-2}$$
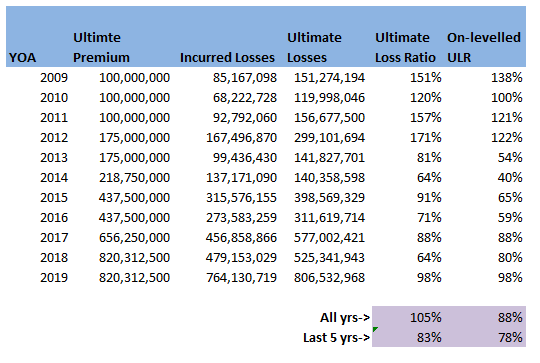
Which we can see quickly approaches infinity as $i$ increases. So for $i$ above $5$, the problem is basically intractable without further improvement. How would we progress if we had to? The only other idea I can come up with is to generate a huge array of all possible passwords (based on brute forcing like above and recording all matches), and then start searching within this array for keywords. We could possibly use some sort of fuzzylookup against a dictionary of keywords. If the original password did not contain any words, but was instead just a fairly random collection of characters then we really would be stumped. I imagine that this problem is basically impossible (and could probably be proved to be so using information theory and entropy) Who invented this algorithm? No idea…I thought it might be fun to do a little bit of online detective work. You see this code all over the internet, but can we find the original source? This site has quite an informative page on the algorithm: https://www.spreadsheet1.com/sheet-protection.html The author of the above page is good enough to credit his source, which is the following stack exchange page: https://superuser.com/questions/45868/recover-sheet-protection-password-in-excel Which in turns states that the code was ‘'Author unknown but submitted by brettdj of www.experts-exchange.com’ I had a quick look on Experts-exchange, but that's as far as I could get, at least we found the guy's username. Can we speed the algorithm up or improve it in any way? I think the current VBA code is basically as quick as it is going to get - the hashing algorithm should work just as fast with a short input as a 12 character input, so starting with a smaller value in the loop doesn’t really get us anything. The only real improvement I can suggest, is that if the Spreadsheet is running too slowly to be able to test a sufficient number of hashes per second, then the hashing algorithm could be implemented in python (which I started to do just out of interest, but it was a bit too fiddly to be fun). Once the algorithm is set up, the password could then be brute forced from there (in much quicker time), and one a valid password has been found, this can then be simply typed into Excel. Should I inflate my loss ratios?14/12/2019 I remember being told as a relatively new actuarial analyst that you "shouldn't inflate loss ratios" when experience rating. This must have been sitting at the back of my mind ever since, because last week, when a colleague asked me basically the same question about adjusting loss ratios for claims inflation, I remembered the conversation I'd had with my old boss and it finally clicked. Let's go back a few years - it's 2016 - Justin Bieber has a song out in which he keeps apologising, and to all of us in the UK, Donald Trump (if you've even heard of him) is still just the America's version of Alan Sugar. I was working on the pricing for a Quota Share, I can't remember the class of business, but I'd been given an aggregate loss triangle, ultimate premium estimates, and rate change information. I had carefully and meticulously projected my losses to ultimate, applied rate changes, and then set the trended and developed losses against ultimate premiums. I ended up with a table that looked something like this: (Note these numbers are completely made up but should give you a gist of what I'm talking about.) I then thought to myself ‘okay this is a property class, I should probably inflate losses by about $3\%$ pa’, the definition of a loss ratio is just losses divided by premium, therefore the correct way to adjust is to just inflate the ULR by $3\%$ pa. I did this, sent the analysis to my boss at the time to review, and was told ‘you shouldn’t inflate loss ratios for claims inflation, otherwise you'd need to inflate the premium as well’ – in my head I was like ‘hmmm, I don’t really get that...’ we’ve accounted for the change in premium by applying the rate change, claims certainly do increase each year, but I don't get how premiums also 'inflate' beyond rate movements?! but since he was the kind of actuary who is basically never wrong and we were short on time, I just took his word for it. I didn’t really think of it again, other than to remember that ‘you shouldn’t inflate loss ratios’, until last week one of my colleagues asked me if I knew what exactly this ‘Exposure trend’ adjustment in the experience rating modelling he’d been sent was. The actuaries who had prepared the work had taken the loss ratios, inflated them in line with claims inflation (what you're not supposed to do), but then applied an ‘exposure inflation’ to the premium. Ah-ha I thought to myself, this must be what my old boss meant by inflating premium. I'm not sure why it took me so long to get to the bottom of what, is when you get down to it, a fairly simple adjustment. In my defence, you really don’t see this approach in ‘London Market’ style actuarial modelling - it's not covered in the IFoA exams for example. Having investigated a little, it does seem to be an approach which is used by US actuaries more – possibly it’s in the CAS exams? When I googled the term 'Exposure Trend', not a huge amount of useful info came up – there are a few threads on Actuarial Outpost which kinda mention it, but after mulling it over for a while I think I understand what is going on. I thought I’d write up my understanding in case anyone else is curious and stumbles across this post. Proof by Example I thought it would be best to explain through an example, let’s suppose we are analysing a single risk over the course of one renewal. To keep things simple, we’ll assume it’s some form of property risk, which is covering Total Loss Only (TLO), i.e. we only pay out if the entire property is destroyed. Let’s suppose for $2018$, the TIV is $1m$ USD, we are getting a net premium rate of $1\%$ of TIV, and we think there is a $0.5\%$ chance of a total loss. For $2019$, the value of the property has increased by $5\%$, we are still getting a net rate of $1\%$, and we think the underlying probability of a total loss is the same. In this case we would say the rate change is $0\%$. That is: $$ \frac{\text{Net rate}_{19}}{\text{Net rate}_{18}} = \frac{1\%}{1\%} = 1 $$ However we would say that claim inflation is $5\%$, which is the increase in expected claims this follows from: $$ \text{Claim Inflation} = \frac{ \text{Expected Claims}_{19}}{ \text{Expected Claims}_{18}} = \frac{0.5\%*1.05m}{0.5\%*1m} = 1.05$$
From first principles, our expected gross gross ratio (GLR) for $2018$ is:
$$\frac{0.5 \% *(TIV_{18})}{1 \% *(TIV_{18})} = 50 \%$$ And for $2019$ is: $$\frac{0.5\%*(TIV_{19})}{1\%*(TIV_{19})} = 50\%$$ i.e. they are the same! The correct adjustment when on-levelling $2018$ to $2019$ should therefore result in a flat GLR – this follows as we’ve got the same GLR in each year when we calculated above from first principles. If we’d taken the $18$ GLR, applied the claims inflation $1.05$ and applied the rate change $1.0$, then we might erroneously think the Gross Loss Ratio would be $50\%*1.05 = 52.5\%$. This would be equivalent to what I did in the opening paragraph of this post, the issue being, that we haven’t accounted for trend in exposure and our rate change is a measure of the change in net rate. If we include this exposure trend as an additional explicit adjustment this gives $50\%*1.05*1/1.05 = 50\%$. Which is the correct answer, as we can see by comparing to our first principles calculation. So the fundamental problem, is that our measure of rate change is a measure in the movement of rate on TIV, whereas our claim inflation is a measure of the movement of aggregate claims. These two are misaligned, if our rate change was instead a measure in the movement of overall premium, then the two measures would be consistent and we would not need the additional adjustment. However it’s much more common in this type of situation to get given rate change as a measure of change in rate on TIV. An advantage of making an explicit adjustment for exposure trend and claims inflation is that it allows us to apply different rates – which is probably more accurate. There’s no a-priori justification as to why the two should always be the same. Claim inflation will be affected by additional factors beyond changes in the inflation of the assets being insured, this may include changes in frequency, changes in court award inflation, etc… It’s also interesting to note that the clam inflation here is of a different nature to what we would expect to see in a standard Collective Risk Model. In that case we inflate individual losses by the average change in severity i.e. ignoring any change in frequency. When adjusting the LR above, we are adjusting for both the change in frequency and severity together, i.e. in the aggregate loss. The above discussion also shows the importance of understanding exactly what someone means by ‘rate change’. It may sound obvious but there are actually a number of subtle differences in what exactly we are attempting to measure when using this concept. Is it change in premium per unit of exposure, is it change in rate per dollar of exposure, or is it even change in rate adequacy? At various points I’ve seen all of these referred to as ‘rate change’. |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
 RSS Feed
RSS Feed