Excel Protect Sheet Encryption

​The original idea for this post came from a slight quirk I noticed in some VBA code I was running (code pasted below) If you've ever needed to remove the protect sheet from a Spreadsheet without knowing the password, then you probably recognise it. 

Sub RemovePassword()

Dim i As Integer, j As Integer, k As Integer
Dim l As Integer, m As Integer, n As Integer
Dim i1 As Integer, i2 As Integer, i3 As Integer
Dim i4 As Integer, i5 As Integer, i6 As Integer
On Error Resume Next
For i = 65 To 66: For j = 65 To 66: For k = 65 To 66
For l = 65 To 66: For m = 65 To 66: For i1 = 65 To 66
For i2 = 65 To 66: For i3 = 65 To 66: For i4 = 65 To 66
For i5 = 65 To 66: For i6 = 65 To 66: For n = 32 To 126
ActiveSheet.Unprotect Chr(i) & Chr(j) & Chr(k) & _
Chr(l) & Chr(m) & Chr(i1) & Chr(i2) & Chr(i3) & _
Chr(i4) & Chr(i5) & Chr(i6) & Chr(n)
If ActiveSheet.ProtectContents = False Then
MsgBox "Password is " & Chr(i) & Chr(j) & _
Chr(k) & Chr(l) & Chr(m) & Chr(i1) & Chr(i2) & _
Chr(i3) & Chr(i4) & Chr(i5) & Chr(i6) & Chr(n)
Exit Sub
End If
Next: Next: Next: Next: Next: Next
Next: Next: Next: Next: Next: Next
End Sub

Nothing too interesting so far, the code looks quite straight forward - we've got a big set of nested loops which appear to test all possible passwords, and will eventually brute force the password - if you've ever tried it you'll know it works pretty well. The interesting part is not so much the code itself, as the answer the code gives - the password which unlocks the sheet is normally something like ‘AAABAABA@1’. I’ve used this code quite a few times over the years, and always with similar results, the password always looks like some variation of this string. This got me thinking - surely it is unlikely that all the Spreadsheets I’ve been unlocking have had passwords of this form? So what’s going on?
 
After a bit of research, it turns out Excel doesn’t actually store the original password, instead it stores a 4-digit hash of the password. Then to unlock the Spreadsheet, Excel hashes the password attempt and compares it to the stored hashed password. Since the size of all possible passwords is huge (full calculations below), and the size of all possible hashes is much smaller, we end up with a high probability of collisions between password attempts, meaning multiple passwords can open a given Spreadsheet.
 
I think the main reason Microsoft uses a hash function in this way rather than just storing the unhashed password is that the hash is stored by Excel as an unencrypted string within a xml file. In fact, an .xlsx file is basically just a zip containing a number of xml files. If Excel didn't first hash the password then you could simply unzip Excel file, find the relevant xml file and read the password from any text editor. With the encryption Excel selected, the best you can do is open the xml file and read the hash of the password, which does not help with getting back to the password due to the nature of the hash function.
 
What hash function is used?
​
I couldn't find the name of the hash anywhere, but the following website has the fullest description I could find of the actual algorithm. As an aside, I miss the days when the internet was made up of websites like this – weird, individually curated, static HTML, obviously written by someone with deep expertise, no ads as well! Here’s the link:
​
http://chicago.sourceforge.net/devel/docs/excel/encrypt.html
​
And the process is as follows:

Here is the algorithm to create the hash value:

1. take the ASCII values of all characters shift left the first character 1 bit, the second 2 bits and so on (use only the lower 15 bits and rotate all higher bits, the highest bit of the 16-bit value is always 0 [signed short])
2. XOR all these values
3. XOR the count of characters
4. XOR the constant 0xCE4B

Example: The password is abcdefghij (10 characters)
a -> 0x61 << 1 == 0x00C2
b -> 0x62 << 2 == 0x0188
c -> 0x63 << 3 == 0x0318
d -> 0x64 << 4 == 0x0640
e -> 0x65 << 5 == 0x0CA0
f -> 0x66 << 6 == 0x1980
g -> 0x67 << 7 == 0x3380
h -> 0x68 << 8 == 0x6800
i -> 0x69 << 9 == 0x5201 (unrotated: 0xD200)
j -> 0x6A << 10 == 0x2803 (unrotated: 0x1A800)
 
count: 0x000A
constant: 0xCE4B
result: 0xFEF1
This value occurs in the PASSWORD record.
​

How many trials will we need to decrypt?

Now we know how the algorithm works, can we come up with a probabilistic bound on the number of trials we would need to check in order to be almost certain to get a collision when carrying out a brute force attack (as per the VBA code above)?

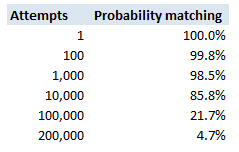
This is a fairly straight forward calculation – the probability of guessing incorrectly for a random attempt is $\frac{1}{65536}$. To keep the maths simple, if we assume independence of attempts, the probability of not getting the password after $n$ attempts is simply: $$ \left( \frac{1}{65536} \right)^n$$ The following table then displays these probabilities

​So we see that with 200,000 trials, there is a less than 5% chance of not having found a match.

We can also derive the answer directly, we are interested in the following probabilistic inequality: $$ \left( 1- \frac{1}{65536} \right)^k < 0.05$$ Taking logs of both sides gives us: $$ln \left( 1- \frac{1}{65536}\right)^k = ln( 0.05)$$ And then bringing down the k: $$k * ln \left( 1- \frac{1}{65536} \right) = ln(0.05)$$ And then solving for $k$: $$k = \frac{ ln(0.05)}{ln \left(1- \frac{1}{65536}\right)} = 196,327$$

Can I work backwards to find the password from a given hash?

As we explained above, in order to decrypt the sheet, you don’t need to find the password, you only need to find a password. Let’s suppose however, for some reason we particularly wanted to find the password which was used, is there any other method to work backwards?

I can only think of two basic approaches:

Option 1 – find an inversion of the hashing algorithm.

Since this algorithm has been around for decades, and is designed to be difficult to reverse, and so far has not been broken, this is a bit of a non-starter. Let me know if you manage it though!

Option 2 – Brute force it.

This is basically your only chance, but let’s run some maths on how difficult this problem is. There are $94$ possible characters (A-Z, a-z,0-9), and in Excel 2010, the maximum password length is $255$, so in all there are, $94^{255}$ possible passwords. Unfortunately for us, that is more than the total number of atoms in the universe $(10^{78})$. If we could check $1000$ passwords per second, then it would take far longer than the current age of the universe to find the correct one.

Okay, so that’s not going to work, but can we make the process more efficient?

Let’s restrict ourselves to looking at passwords of a known length. Suppose we know the password is only a single character, in that case we simply need to check $94$ possible passwords, one of which should unlock the sheet, hence giving us our password. In order to extend this reasoning to passwords of arbitrary but known length, let’s think of the hashing algorithm as a function and consider its domain and range: Let’s call our hashing algorithm $F$, the set of all passwords of length $i$, $A_i$, and the set of all possible password hashes $B$. Then we have a function:
$$ F: A_i -> B$$
Now if we assume the algorithm is approximately equally spread over all the possible values of $B$, then we can use the size of $B$ to calculate the size of the kernel $F^{-1}[A_i]$. The size of $B$ doesn’t change. Since we have a $4$ digit hexadecimal, it is of size $16^4$, and since we know the size of $A_i$ is $96$, we can then estimate the size of the kernel.

Let’s take $i=4$, and work it through:

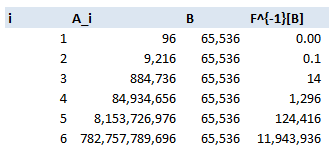
$A_4$ is size $96^4 = 85m$, $B = 65536$, hence $|F^{-1}[A_4]| = \frac{85m}{65536} = 124416$

Which means for every hash, there are $124,416$ possible $4$ digit passwords which can create this hash, and therefore may have been the original password.

​Here is a table of the values for $I = 1$ to $6$:

In fact we can come up with a formula for size of the kernel: $$\frac{96^i}{16^4} \sim 13.5 * 96^{i-2}$$

Which we can see quickly approaches infinity as $i$ increases.

So for $i$ above $5$, the problem is basically intractable without further improvement. How would we progress if we had to? The only other idea I can come up with is to generate a huge array of all possible passwords (based on brute forcing like above and recording all matches), and then start searching within this array for keywords. We could possibly use some sort of fuzzylookup against a dictionary of keywords.

If the original password did not contain any words, but was instead just a fairly random collection of characters then we really would be stumped. I imagine that this problem is basically impossible (and could probably be proved to be so using information theory and entropy)

Who invented this algorithm?

No idea…I thought it might be fun to do a little bit of online detective work. You see this code all over the internet, but can we find the original source?

This site has quite an informative page on the algorithm:
https://www.spreadsheet1.com/sheet-protection.html

The author of the above page is good enough to credit his source, which is the following stack exchange page:
https://superuser.com/questions/45868/recover-sheet-protection-password-in-excel

Which in turns states that the code was ‘'Author unknown but submitted by brettdj of www.experts-exchange.com’

I had a quick look on Experts-exchange, but that's as far as I could get, at least we found the guy's username.

Can we speed the algorithm up or improve it in any way?

I think the current VBA code is basically as quick as it is going to get - the hashing algorithm should work just as fast with a short input as a 12 character input, so starting with a smaller value in the loop doesn’t really get us anything. The only real improvement I can suggest, is that if the Spreadsheet is running too slowly to be able to test a sufficient number of hashes per second, then the hashing algorithm could be implemented in python (which I started to do just out of interest, but it was a bit too fiddly to be fun). Once the algorithm is set up, the password could then be brute forced from there (in much quicker time), and one a valid password has been found, this can then be simply typed into Excel.