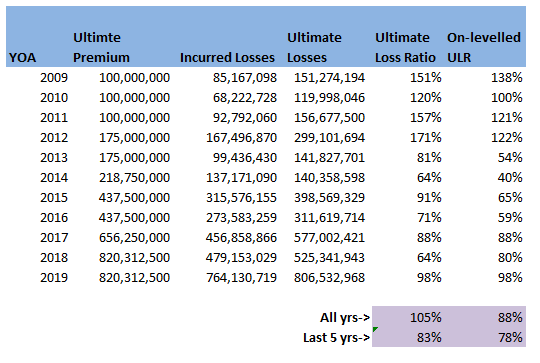
Should I inflate my loss ratios?

​I remember being told as a relatively new actuarial analyst that you "shouldn't inflate loss ratios" when experience rating. This must have been sitting at the back of my mind ever since, because last week, when a colleague asked me basically the same question about adjusting loss ratios for claims inflation, I remembered the conversation I'd had with my old boss and it finally clicked.

Let's go back a few years - it's 2016 - Justin Bieber has a song out in which he keeps apologising, and  to all of us in the UK, Donald Trump (if you've even heard of him) is still just the America's version of Alan Sugar. I was working on the pricing for a Quota Share, I can't remember the class of business, but I'd been given an aggregate loss triangle, ultimate premium estimates, and rate change information. I had carefully and meticulously projected my losses to ultimate, applied rate changes, and then set the trended and developed losses against ultimate premiums. I ended up with a table that looked something like this:

(Note these numbers are completely made up but should give you a gist of what I'm talking about.)

I then thought to myself ‘okay this is a property class, I should probably inflate losses by about $3\%$ pa’, the definition of a loss ratio is just losses divided by premium, therefore the correct way to adjust is to just inflate the ULR by $3\%$ pa. I did this, sent the analysis to my boss at the time to review, and was told ‘you shouldn’t inflate loss ratios for claims inflation, otherwise you'd need to inflate the premium as well’ – in my head I was like ‘hmmm, I don’t really get that...’ we’ve accounted for the change in premium by applying the rate change, claims certainly do increase each year, but I don't get how premiums also 'inflate' beyond rate movements?! but since he was the kind of actuary who is basically never wrong and we were short on time, I just took his word for it.

I didn’t really think of it again, other than to remember that ‘you shouldn’t inflate loss ratios’, until last week one of my colleagues asked me if I knew what exactly this ‘Exposure trend’ adjustment in the experience rating modelling he’d been sent was. The actuaries who had prepared the work had taken the loss ratios, inflated them in line with claims inflation (what you're not supposed to do), but then applied an ‘exposure inflation’ to the premium. Ah-ha I thought to myself, this must be what my old boss meant by inflating premium.

I'm not sure why it took me so long to get to the bottom of what, is when you get down to it, a fairly simple adjustment. In my defence, you really don’t see this approach in ‘London Market’ style actuarial modelling - it's not covered in the IFoA exams for example. Having investigated a little, it does seem to be an approach which is used by US actuaries more – possibly it’s in the CAS exams?

When I googled the term 'Exposure Trend', not a huge amount of useful info came up – there are a few threads on Actuarial Outpost which kinda mention it, but after mulling it over for a while I think I understand what is going on. I thought I’d write up my understanding in case anyone else is curious and stumbles across this post.

Proof by Example

I thought it would be best to explain through an example, let’s suppose we are analysing a single risk over the course of one renewal. To keep things simple, we’ll assume it’s some form of property risk, which is covering Total Loss Only (TLO), i.e. we only pay out if the entire property is destroyed.

Let’s suppose for $2018$, the TIV is $1m$ USD, we are getting a net premium rate of $1\%$ of TIV, and we think there is a $0.5\%$ chance of a total loss. For $2019$, the value of the property has increased by $5\%$, we are still getting a net rate of $1\%$, and we think the underlying probability of a total loss is the same.

In this case we would say the rate change is $0\%$. That is:

$$ \frac{\text{Net rate}_{19}}{\text{Net rate}_{18}} = \frac{1\%}{1\%} = 1 $$

However we would say that claim inflation is $5\%$, which is the increase in expected claims this follows from:

$$ \text{Claim Inflation} = \frac{ \text{Expected Claims}_{19}}{ \text{Expected Claims}_{18}} = \frac{0.5\%*1.05m}{0.5\%*1m} = 1.05$$

From first principles, our expected gross gross ratio (GLR) for $2018$ is:
$$\frac{0.5 \% *(TIV_{18})}{1 \% *(TIV_{18})} = 50 \%$$ And for $2019$ is: $$\frac{0.5\%*(TIV_{19})}{1\%*(TIV_{19})} = 50\%$$
i.e. they are the same!

The correct adjustment when on-levelling $2018$ to $2019$ should therefore result in a flat GLR – this follows as we’ve got the same GLR in each year when we calculated above from first principles. If we’d taken the $18$ GLR, applied the claims inflation $1.05$ and applied the rate change $1.0$, then we might erroneously think the Gross Loss Ratio would be $50\%*1.05 = 52.5\%$. This would be equivalent to what I did in the opening paragraph of this post, the issue being, that we haven’t accounted for trend in exposure and our rate change is a measure of the change in net rate. If we include this exposure trend as an additional explicit adjustment this gives $50\%*1.05*1/1.05 = 50\%$. Which is the correct answer, as we can see by comparing to our first principles calculation.

So the fundamental problem, is that our measure of rate change is a measure in the movement of rate on TIV, whereas our claim inflation is a measure of the movement of aggregate claims. These two are misaligned, if our rate change was instead a measure in the movement of overall premium, then the two measures would be consistent and we would not need the additional adjustment. However it’s much more common in this type of situation to get given rate change as a measure of change in rate on TIV.
​
An advantage of making an explicit adjustment for exposure trend and claims inflation is that it allows us to apply different rates – which is probably more accurate. There’s no a-priori justification as to why the two should always be the same. Claim inflation will be affected by additional factors beyond changes in the inflation of the assets being insured, this may include changes in frequency, changes in court award inflation, etc…

It’s also interesting to note that the clam inflation here is of a different nature to what we would expect to see in a standard Collective Risk Model. In that case we inflate individual losses by the average change in severity i.e. ignoring any change in frequency. When adjusting the LR above, we are adjusting for both the change in frequency and severity together, i.e. in the aggregate loss.

The above discussion also shows the importance of understanding exactly what someone means by ‘rate change’. It may sound obvious but there are actually a number of subtle differences in what exactly we are attempting to measure when using this concept. Is it change in premium per unit of exposure, is it change in rate per dollar of exposure, or is it even change in rate adequacy? At various points I’ve seen all of these referred to as ‘rate change’.