Making people smarter by designing a more efficient number system

Designing a new number system

I got interested in alternative number systems when I read Malcolm Gladwell's book Outliers back in uni. You might be surprised that Gladwell would write about this topic, but he actually uses it to attempt to explain why Asian students tend to do so well at maths in the US. I was flicking through an old notebook the other day and I can across my attempt at designing such a system. I thought it might be interesting to write up my system. 

To set the scene, here is the relevant extract from the book:

"Take a look at the following list of numbers: 4,8,5,3,9,7,6. Read them out loud to yourself. Now look away, and spend twenty seconds memorizing that sequence before saying them out loud again.If you speak English, you have about a 50 percent chance of remembering that sequence perfectly If you’re Chinese, though, you’re almost certain to get it right every time. Why is that? Because as human beings we store digits in a memory loop that runs for about two seconds. We most easily memorize whatever we can say or read within that two second span. And Chinese speakers get that list of numbers—4,8,5,3,9,7,6—right every time because—unlike English speakers—their language allows them to fit all those seven numbers into two seconds.

That example comes from Stanislas Dehaene’s book “The Number Sense,” and as Dehaene explains:
Chinese number words are remarkably brief. Most of them can be uttered in less than one-quarter of a second (for instance, 4 is ‘si’ and 7 ‘qi’) Their English equivalents—”four,” “seven”—are longer: pronouncing them takes about one-third of a second. The memory gap between English and Chinese apparently is entirely due to this difference in length. In languages as diverse as Welsh, Arabic, Chinese, English and Hebrew, there is a reproducible correlation between the time required to pronounce numbers in a given language and the memory span of its speakers. In this domain, the prize for efficacy goes to the Cantonese dialect of Chinese, whose brevity grants residents of Hong Kong a rocketing memory span of about 10 digits.

It turns out that there is also a big difference in how number-naming systems in Western and Asian languages are constructed. In English, we say fourteen, sixteen, seventeen, eighteen and nineteen, so one would think that we would also say one-teen, two-teen, and three-teen. But we don’t. We make up a different form: eleven, twelve, thirteen, and fifteen. Similarly, we have forty, and sixty, which sound like what they are. But we also say fifty and thirty and twenty, which sort of sound what they are but not really. And, for that matter, for numbers above twenty, we put the “decade” first and the unit number second: twenty-one, twenty-two. For the teens, though, we do it the other way around. We put the decade second and the unit number first: fourteen, seventeen, eighteen. The number system in English is highly irregular. Not so in China, Japan and Korea. They have a logical counting system. Eleven is ten one. Twelve is ten two. Twenty-four is two ten four, and so on.
That difference means that Asian children learn to count much faster. Four year old Chinese children can count, on average, up to forty. American children, at that age, can only count to fifteen, and don’t reach forty until they’re five: by the age of five, in other words, American children are already a year behind their Asian counterparts in the most fundamental of math skills.

The regularity of their number systems also means that Asian children can perform basic functions—like addition—far more easily. Ask an English seven-year-old to add thirty-seven plus twenty two, in her head, and she has to convert the words to numbers (37 + 22). Only then can she do the math: 2 plus 7 is nine and 30 and 20 is 50, which makes 59. Ask an Asian child to add three-tens-seven and two tens-two, and then the necessary equation is right there, embedded in the sentence. No number translation is necessary: It’s five-tens nine.

“The Asian system is transparent,” says Karen Fuson, a Northwestern University psychologist, who has done much of the research on Asian-Western differences. “I think that it makes the whole attitude toward math different. Instead of being a rote learning thing, there’s a pattern I can figure out. There is an expectation that I can do this. There is an expectation that it’s sensible. For fractions, we say three fifths. The Chinese is literally, ‘out of five parts, take three.’ That’s telling you conceptually what a fraction is. It’s differentiating the denominator and the numerator.”

The much-storied disenchantment with mathematics among western children starts in the third and fourth grade, and Fuson argues that perhaps a part of that disenchantment is due to the fact that math doesn’t seem to make sense; its linguistic structure is clumsy; its basic rules seem arbitrary and complicated.

Asian children, by contrast, don’t face nearly that same sense of bafflement. They can hold more numbers in their head, and do calculations faster, and the way fractions are expressed in their language corresponds exactly to the way a fraction actually is—and maybe that makes them a little more likely to enjoy math, and maybe because they enjoy math a little more they try a little harder and take more math classes and are more willing to do their homework, and on and on, in a kind of virtuous circle.

When it comes to math, in other words, Asians have built-in advantage. . ."

Here's a link to Gladwell's website which contains the extract.
gladwell.com/outliers/rice-paddies-and-math-tests/

Base-10 System

Gladwell mainly talks about the words that the Chinese use for numbers and the structure inherent in them, but there is actually another more interesting way we can embed structure in our number system.

Our current number system is base-10, which means that we have different symbols for all the numbers up to 10 (0,1,2,3,4,...,9), and then when we get to the number 10, we use the first number again but we move it over one place, and then put a zero in it's place. When we are teaching a child how to write numbers, this is exactly how we explain it to them. For example to write two hundred and seven, we would tell them that they need to put a 2 in the hundreds columns a 0 in the tens column and a 7 in the units column - 207.

The fact that we use a base-10 number system is actually just a historical quirk. The only reason humans started to use it is just that we have 10 fingers, there's no particular mathematical benefit to a base-10 system. We could actually base our number system on any integer. The most commonly used alternative is the binary number system used extensively in computing. The binary number system is a base-2 number system where we only have 2 symbols - 0 and 1. The trick is that instead of reusing the first symbol when we get to ten, we do it when we get to two. So the sequence of numbers up to 10 in binary is:

In fact we don't even need to restrict ourselves to integers as the base of our number system. For example, we could even use base $ \pi $! Under this system if we want to write $ \pi $, then we would just write 1, to write $ \pi^2 $ it would just be 10. Writing one in base $ \pi $ would be quite difficult though, and we would need to either write $ 1 / {\pi} $ or invent a new character.



Base 12 number system

So what would be the ideal number on which to base our number system?

I'm going to make the argument that a base 12 number system would be the best option. 12 has a large number of small factors and this makes it ideal as a base.

• 12 has almost twice as many prime factors as 10. When working in base 10, it is relatively easy to multiply a number by either 2, 5, or 10, this is because these are all factors of 10. When we are working in base 12, it will be easy to multiply by 2, 3, 4, 6, and 12. Division by these numbers is also much easier. 
• It is the smallest number divisible by 1,2,3, and 4.
• We seem to intuitively favour the number 12 in many common circumstances. It has it's own name - a dozen, we also used it to split inches into feet. It's actually the largest integer that has still has it's own name. Once we get to 13, it's just a combination of three and teen, and so on for larger numbers, but eleven and twelve have their own names.
• We have 12 knuckles on the four fingers of each hand (ignoring thumbs) making counting on our hands easy still.

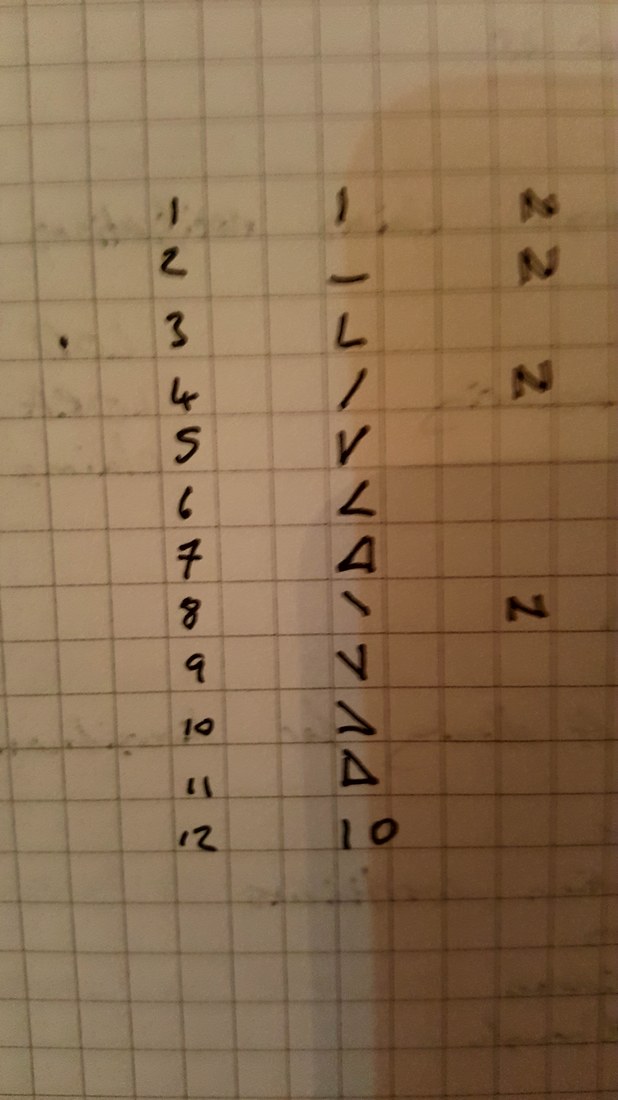
Returning back to Gladwell's idea, another change we could make to the number system to help make it more structured is to change the actual symbols we use for the integers. Here was my attempt from 2011 for alternative symbols we could use.

My approach was to embed as much structure into the numbers as possible, so the symbol for three is actually just a combination of the symbols for one and two. This applies for all the numbers other than one, two, four, and eight.

I wonder if it would be possible to come up with some sort of rule about how the symbols rotate to further reduce the total number of symbols and also to add some additional structure to the symbols.

Let me know if you can think of any additional improvements that could be made to our number system.
​