Estimation of Standard Deviation - Why is it so difficult?

I could be on my own here, but personally I always thought the definition of Sample Standard Deviation is pretty ugly.
$$ \sqrt {\frac{1}{n - 1} \sum_{i=1}^{n} { ( x_i - \bar{x} )}^2 } $$
We've got a square root involved which can be problematic, and what's up with the $\frac{1}{n-1}$? Especially the fact that it's inside the square root, also why do we even need a separate definition for a sample standard deviation rather than a population standard deviation?

When I looked into why we do this, it turns out that the concept of sample standard deviation is actually a bit of a mess. 

Before we tear it apart too much though, let's start by looking at some of the properties of  standard deviation which are good.

Advantages of Standard Deviation
​

• Unlike the variance, the standard deviation is in the same units as the mean. For example, if we are measuring the height of people in meters, if we take the mean, then the units will also be in meters (which probably sounds so obvious you wouldn't even think about it), the variance of heights on the other hand will be in meters squared which can be problematic. This is why we use the standard deviation which will convert the units back to meters.
• We can fully characterise many distributions by just specifying the mean and standard deviation. This is the case for many major distributions for example the Normal Distribution, Log-normal, Exponential, etc.
• In order to compare the variability of two distributions, we need a dimensionless quantity representing variability which is not effected by the absolute size of the underlying data. For example, if we are trying to answer the question: 'which has more variability, human height, or dog height', then if we just look at the variance of both of these, since humans are much taller in general the variance will also be greater and we might mistakenly believe that there is more variability in human height. If instead we look at the Coefficient of Variation, which is defined to be Standard Deviation over Mean, then this will be unaffected by the greater average human height and we would find out that there is actually greater relative variability in dog size (I would guess this is the case, but I've not actually checked it).
• The Sample Standard Deviation is an unbiased estimator of the population standard Deviation.

​
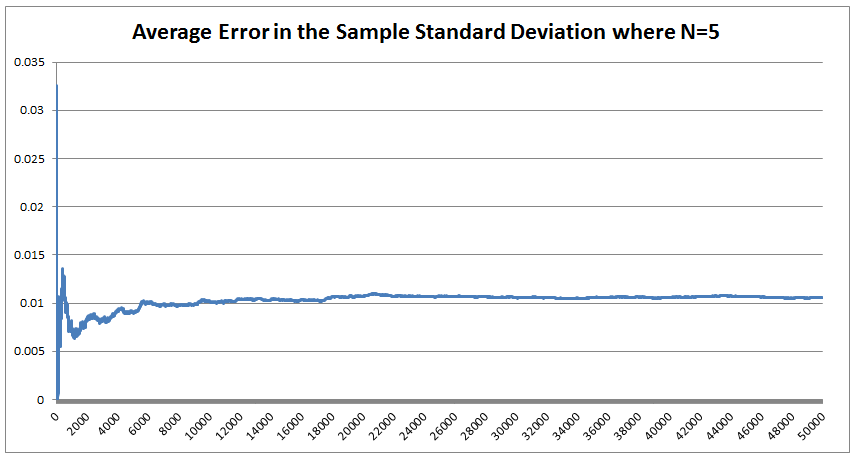
The last property is a really important one. The $\frac{1}{n-1}$ factor is a correction we make which we are told turns the sample standard deviation into an unbiased estimator of the population standard deviation. We can test this pretty easily, I sampled 50,000 simulations from a probability distribution and then measured the squared difference between the mean of the sample standard deviation and the actual value computed analytically.​​

We see that the Average Error converges quite quickly but for some reason it doesn't converge to 0 as expected!

It turns out that the usual formula for the sample standard deviation is not actually an unbiased estimator of the population standard deviation after all. I'm pretty sure they never mentioned that in my stats lectures at uni. The $n-1$ correction changes the formula for sample variance into an unbiased estimator, and the formula we use for the sample standard deviation is just the square root of the unbiased estimator for variance. If we do want an unbiased estimator for the sample standard deviation then we need to make an adjustment based not just on the sample size, but also the underlying distribution. Which in many cases we are not going to know at all.

The wiki page has a good summary of the problem, and also has formulas for the unbiased estimator of the sample standard deviation:
en.wikipedia.org/wiki/Unbiased_estimation_of_standard_deviation
​
Just to give you a sense of the complexity, here is the factor that we need to apply to the usual definition of sample standard deviation in order to have an unbiased estimator for a normal distribution.
$$ \frac {1} {    \sqrt{  \frac{2}{n-1}   }  \frac{  \Gamma \Big( \frac{ n } {2} \Big) }  {\Gamma \Big(  \frac{n-1}{2} \Big)}   }  $$

Where $\Gamma$ is the Gamma function.

​Alternatives to Standard Deviation

Are there any obvious alternatives to using standard deviation as our default measure of variability? Nassim Nicholas Taleb, author of Black Swan, is also not a fan of the wide spread use of the standard deviation of a distribution as a measure of its volatility. Taleb has different issues with it, mainly around the fact that it was often overused in banking by analysts who thought it completely characterised volatility. So for example, when modelling investment returns, an analyst would look at the sample standard deviation, and then assume the investment returns follow a Lognormal distribution with this standard deviation, when we should actually be modelling returns with a much fatter tailed distributions. So his issue was the fact that people believed that they were fully characterising volatility in this way, when they should have also been considering kurtosis and higher moments or considering fatter tailed distributions. Here is a link to Taleb's rant which is entertaining as always:

www.edge.org/response-detail/25401

Taleb's suggestion is a different statistic called Mean Absolute Deviation the definition is.
$$\frac{1}{n} \sum_{i=1}^n | x_i - \bar{x} | $$

We can see immediately why mathematicians prefer to deal with the standard deviation instead of the mean absolute deviation, working with sums of absolute values is normally much more difficult analytically than working with the square root of the sum of squares. In the ages of ubiquitous computing though, this should probably be a smaller consideration.