Poisson Distribution - What is the Probability the Distribution is equal to its Mean?

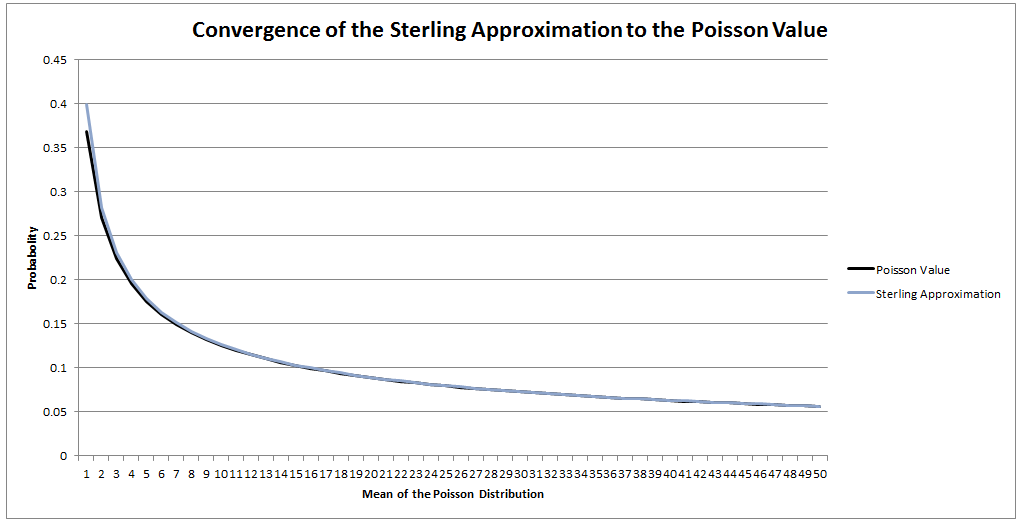
​I saw a cool trick the other day involving the Poisson Distribution and Stirling's Approximation.

Given a Poisson Distribution $ N  $ ~ $ Poi( \lambda ) $

The probability that $N$ is equal to a given $n$ is defined to be:

$$P ( N = n) = \frac { {\lambda}^n e^{-n} } {n! } $$
What is the probability that $N$ is equal to it's mean? In this case, let's use $n$ as the mean of the distribution for reasons that will become clear later.

Plugging $n$ into the definition of the Poisson distribution gives:

$$P ( N = n) = \frac { n^n e^{-n} } {n! } $$
At this point, we use Sterling's approximation. Which states that for large $n$:

                                                             $n!$  ~ $ {\left( \frac { n } {e } \right) }^n \frac { 1 } { \sqrt{ 2 \pi n } }$

Plugging this into the definition of the Poission Distribution gives:

$$P ( N = n) = \frac { n^n e^{-n} } {{\left( \frac { n } {e } \right) }^n} \frac { 1 } { \sqrt{ 2 \pi n } } $$
Which simplifies to:

$$P ( N = n) = \frac { 1 } { \sqrt{ 2 \pi n } } $$

So for large $n$ we end up with a nice result for the Probability that a Poisson Distribution will end up being equal to it's Expected Value.

Convergence

The convergence of the series is actually really quick. I checked the convergence for n between 1 and 50, and even by n=5, the approximation is very close, when I graphed it, the lines become indistinguishable very quickly.
​