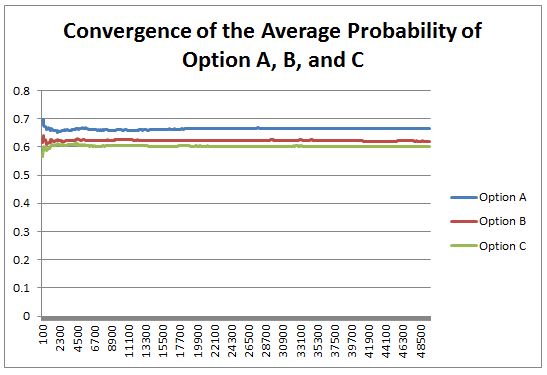
The Newton - Pepys Problem17/6/2017 I always found it quite interesting that prior to the 19th century, Probability Theory was basically just a footnote to the study of gambling. The first time that Probability Theory was formalised in any systematic way at all was through the correspondence of three 17th century mathematicians, Pierre Fermat (famous for his last theorem), Blaise Pascal (famous for his wager), and Gerolamo Cardano (not actually famous at all) when analysing a problem in gambling called the problem of points. The problem of points is the problem of how to come up with a fair way to divide the winnings when betting on a game of chance which has interrupted before it can be finished. For example, let's say we are playing a game where we take it in turns to roll a dice and we record how many 6s we get, the first person who rolls a total of 10 6s wins. What happens if we are unable to finish the game, but one player has already rolled 8 6s, whereas their opponent has only rolled 2 6s. How should we divide the money in a fair way? Obviously it's unfair to just split the money 50-50 as the player with 8 6s has a much higher chance of winning, but at the same time, there is a chance that the player with only 2 6s might get lucky and still win, so we can't just give all the money to the player who is currently winning. The solution to the problem involves calculating the probability of each player winning given their current state, and then dividing the money proportionally. In order to answer this question in a systematic way, Fermat, Pascal, and Cardano formalised many of the basic principles of Probability Theory which we still use today. Newton - Pepys Problem The Newton - Pepys problem is another famous problem related to gambling and Probability Theory. It is named after a series of correspondence between Isaac Newton and Samuel Pepys, the famous diarist, in 1693. Pepys wrote to Newton asking for his opinion on a wager that he wanted to make. Which of the following three propositions has the greatest chance of success? A. Six fair dice are tossed independently and at least one “6” appears. B. Twelve fair dice are tossed independently and at least two “6”s appear. C. Eighteen fair dice are tossed independently and at least three “6”s appear. Pepys initially believed that Option C had the highest chance of success, followed by Option B, then Option A. Newton correctly answered that it was in fact the opposite order and that Option A was the most likely, Option C was the least likely. Wikipedia has the analytical solution to the problem. Which comes out as: There's a few things I find really interesting about Newton and Pepys's exchange. The first is that it's cool to think of two very different historical figures such as Newton and Pepys being acquainted and corresponding with each other. For me, it makes them much more human and brings them to life the fact that they were both living in London and moving in the same social circles at the same time. Another interesting point is that once again, we see that Probability Theory has been advanced again due to the desire to make money from Gambling. Finally I think it's cool that Pepys was able to ask one of the greatest physicists of all time for a solution to the problem, yet the solution is trivial now. Luckily Newton was able to provide Pepys with an answer, though it might have taken Newton quite a while to calculate, especially for Option C. But you could give the problem to any student now who has access to a computer and they would be able to give you an answer in minutes by just simulating the problem stochastically. Stochastic modelling always seemed like a new form of empiricism to me, whereas calculating the answer with a computer analytically still seems like a-priori reasoning. Newton probably did compute the answer analytically by hand, but he would not have been able to simulate 50,000 simulations of the game by hand. It's fundamentally a different kind of reasoning, and the closest he could have got would have been to play the game 50,000 times and record the average. Stochastic Model To calculate this myself I set up a Monte Carlo model of the game and simulated 50,000 rolls of the dice to calculate the expected probability of each of these three options. We can clearly see from this graph that Option A is the most likely Option of the three, with Option C being the least likely. We can tell all of this by just setting up a model that takes 5 minutes to build and give an answer in seconds. It makes you wonder what Newton would have been able to manage if he had access to the computing power that we take for granted now. Sources: Wikipedia: en.wikipedia.org/wiki/Newton%E2%80%93Pepys_problem An Article by Stephen Stigler: arxiv.org/pdf/math/0701089.pdf |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
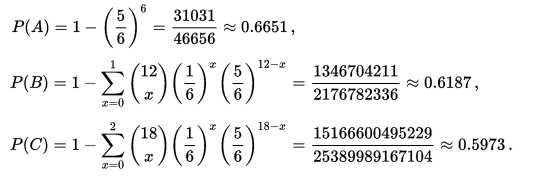
 RSS Feed
RSS Feed
Leave a Reply.