Monte Carlo Tic Tac Toe Engine

Since setting up the approximation of $\pi$ using the Monte Carlo technique of sampling inside a circle, I've been playing around with applying Monte Carlo methods to other problems.

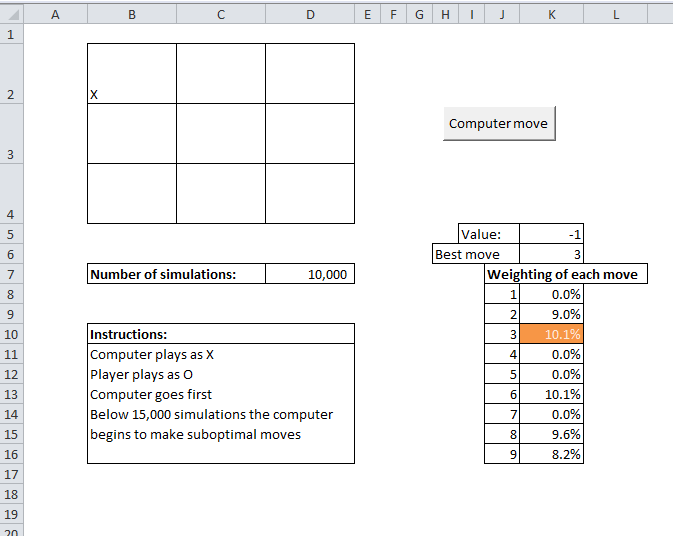
One problem I thought it would be fun to play around with was creating an AI engine that uses Monte Carlo rather than deterministic methods to run. My first thought was to look at a chess engine, I've always wanted to set one up, but after playing around with it for a while I realised setting up the actual game engine was going to be a substantial amount of work before even thinking about the AI. Therefore I shelved that for the time being.

The next game I decided to look at Tic-Tac-Toe or Noughts and Crosses which is on the opposite end of the spectrum in terms of complexity of rules.

Optimal Strategies

As every school age kid quickly learns, there is an optimal strategy for playing Tic-Tac-Toe. In case anyone has forgotten it can easily found online, however programming in the strategy would have been quite tedious, and not as fun as messing around with a stochastic solution.

I thought it was interesting that a Monte Carlo engine, if it can be programmed to play the game well without even being told what the optimal strategy is, should replicate this strategy simply by selecting what it believes is the optimal move based on its own analysis. It can do all of this without ever truly knowing what the strategy is.

I decided to write the engine in VBA, which is not a great development language generally. But meant that I could stick the game into a Spreadsheet which seemed like a fun thing to do. Here's a screenshot of the game:

How it works

The way the engine works is each time the computer is about to move, it uses the current state of the grid, and plays out a large number of random games (for each move it makes a random selection for itself and then a random selection for the player until one side wins or it is a draw).

The computer tracks who wins each game and more importantly, for each of the possible next moves for the computer, whether it eventually ends in a win, draw or loss. The computer repeats this process a large number of times (the default being 10,000), each time assigning a value to the starting move of +1 if the computer eventually wins the game, +0.5 if the game ends in a draw, and 0 if the computer losses the game. The computer keeps a running total of the value assigned to each starting move. Once the simulation of random games is completed, the computer selects the move with the highest value, this should correspond to the starting move that is the most likely to led to a victory or a draw,

I've linked below to the Excel file with the game inside:

tic_tac_toe.xlsm
File Size:	26 kb
File Type:	xlsm

Download File

---

​And here is the source code in VBA:​

Hide Code

Option Base 1
Option Explicit

Sub MakeMove()

Dim vGrid As Variant
Dim vGridPerm As Variant

Dim iNewCell As Integer
Dim iFirstMove As Integer
Dim irow As Integer

Dim lSimNum As Long
Dim lNumSim As Long

Dim vNextmove(9) As Long

lNumSim = Range("NumSim")
vGrid = Range("Grid")
vGridPerm = Range("Grid")

If CheckWin(vGrid) <> -1 Then
    Exit Sub
End If

For lSimNum = 1 To lNumSim
    
    vGrid = vGridPerm
    
    iFirstMove = GetRandom(vGrid)
    vGrid(iCellToiRow(iFirstMove), iCellToiCol(iFirstMove)) = "X"
    
    While CheckWin(vGrid) = -1
        iNewCell = GetRandom(vGrid)
        vGrid(iCellToiRow(iNewCell), iCellToiCol(iNewCell)) = "O"
        iNewCell = GetRandom(vGrid)
        vGrid(iCellToiRow(iNewCell), iCellToiCol(iNewCell)) = "X"
    Wend

    vNextmove(iFirstMove) = vNextmove(iFirstMove) + CheckWin(vGrid)
    
Next

Range("k6") = findmax(vNextmove)
For irow = 1 To 9
    Range("k7").Offset(irow, 0) = (vNextmove(irow) / lNumSim)
Next

vGridPerm(iCellToiRow(findmax(vNextmove)), iCellToiCol(findmax(vNextmove))) = "X"

Range("grid") = vGridPerm

End Sub

Function findmax(vNextmove)

Dim iCell As Integer
Dim iMax(2) As Integer

iMax(1) = 1

For iCell = 1 To 9
    If vNextmove(iCell) > iMax(1) Then
        iMax(1) = vNextmove(iCell)
        iMax(2) = iCell
    End If
Next

findmax = iMax(2)

End Function

Function GetRandom(vGrid As Variant)

Dim iCell As Integer
Dim iCountBlank As Integer
Dim vEmpty(9) As Variant

iCountBlank = 0

For iCell = 1 To 9
    If vGrid(iCellToiRow(iCell), iCellToiCol(iCell)) = "" Then
        vEmpty(iCountBlank + 1) = iCell
        iCountBlank = iCountBlank + 1
    End If
Next

Randomize
GetRandom = vEmpty(Int(Rnd * (iCountBlank) + 1))

End Function

Function iCellToiRow(iCell As Integer)

iCellToiRow = 1 + Int((iCell - 1) / 3)

End Function

Function iCellToiCol(iCell As Integer)

iCellToiCol = 1 + ((iCell - 1) Mod 3)

End Function

Function CheckWin(vGrid As Variant)

Dim irow As Integer
Dim iCol As Integer
Dim iDiag As Integer

Dim iCountX As Integer
Dim iCountO As Integer
Dim iCountBoth As Integer

'1 = win, 1/2 = draw, 0=Lose, -1 = continuing

' Check X then O
' Check Rows, Check Columns, check down diag, check up diag

CheckWin = -1

For irow = 1 To 3
    iCountX = 0
    iCountO = 0
    For iCol = 1 To 3
        If vGrid(irow, iCol) = "X" Then
            iCountX = iCountX + 1
        End If
        If vGrid(irow, iCol) = "O" Then
            iCountO = iCountO + 1
        End If
    Next
    If iCountX = 3 Then
        CheckWin = 1
        Exit Function
    ElseIf iCountO = 3 Then
        CheckWin = 0
        Exit Function
    End If
Next


For iCol = 1 To 3
    iCountX = 0
    iCountO = 0
    For irow = 1 To 3
        If vGrid(irow, iCol) = "X" Then
            iCountX = iCountX + 1
        End If
        If vGrid(irow, iCol) = "O" Then
            iCountO = iCountO + 1
        End If
    Next
    If iCountX = 3 Then
        CheckWin = 1
        Exit Function
    ElseIf iCountO = 3 Then
        CheckWin = 0
        Exit Function
    End If
Next

iCountX = 0
iCountO = 0
For iDiag = 1 To 3
    If vGrid(iDiag, iDiag) = "X" Then
        iCountX = iCountX + 1
    End If
    If vGrid(iDiag, iDiag) = "O" Then
        iCountO = iCountO + 1
    End If
    If iCountX = 3 Then
        CheckWin = 1
        Exit Function
    ElseIf iCountO = 3 Then
        CheckWin = 0
        Exit Function
    End If
Next

iCountX = 0
iCountO = 0
For iDiag = 1 To 3
    If vGrid(iDiag, 4 - iDiag) = "X" Then
        iCountX = iCountX + 1
    End If
    If vGrid(iDiag, 4 - iDiag) = "O" Then
        iCountO = iCountO + 1
    End If
    If iCountX = 3 Then
        CheckWin = 1
        Exit Function
    ElseIf iCountO = 3 Then
        CheckWin = 0
        Exit Function
    End If
Next

iCountBoth = 0
For irow = 1 To 3
    For iCol = 1 To 3
        If vGrid(irow, iCol) = "X" Or vGrid(irow, iCol) = "O" Then
            iCountBoth = iCountBoth + 1
        End If
    Next
Next

If iCountBoth = 9 Then
    CheckWin = 0.5
    Exit Function
End If

End Function
 

Show Code

Future Development

Something that I would like to explore in the future is the use of more efficient algorithms for analysing the best move. For example, apparently alpha-beta pruning can be used to focus on the moves that look the most promising rather than spending an equal amount of time looking at all moves.

​I would also like to make a web based version of the game at some point.,