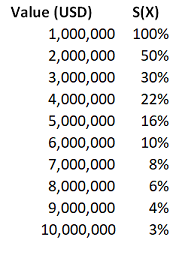
Excess layer pricing16/9/2020 I had to solve an interesting problem yesterday relating to pricing an excess layer which was contained in another layer which we knew the price for – I didn’t price the initial layer, and I did not have a gross loss model. All I had to go on was the overall price and a severity curve which I thought was reasonably accurate. The specific layers in this case were a 9m xs 1m, and I was interested in what we would charge for a 6m xs 4m. Just to put some concrete numbers to this, let’s say the 9m xs 1m cost \$10m The xs 1m severity curve was as follows: Which we can convert into a survival function for xs 4m as follows: Pricing the layer
We can reason as follows, we are interested in: $$ \text{Price}_{\text{6 xs 4}} = \text{(freq xs 4)(average loss to layer s.t. loss xs 4)/(loss ratio)} $$ And we know the following: $$ \text{Price}_{\text{9 xs 1}} = \text{(freq xs 1)(average loss to layer s.t. loss xs 1)/(loss ratio)} = 10m$$ Solving for freq xs 1: $$ \text{(freq xs 1)} = \frac{10m}{\text{(average loss to layer s.t. loss xs 1)/(loss ratio)}} $$ And then noting that $ \text{freq xs 4} = \text{freq xs 1} * S(4) = \text{freq xs 1} * 22\% $, which when combined with the above gives us: $$\text{Price}_{\text{6 xs 4}} = \frac{10m}{\text{(average loss to layer s.t. loss xs 1)}/\text{(loss ratio)}} * 22\% * \text{(average loss to layer s.t. loss xs 4)} * \text{(loss ratio)} $$ And then, rearranging and cancelling the loss ratios: $$\text{Price}_{\text{6 xs 4}} = 10m * 22\% \frac{\text{(average loss to layer s.t. loss xs 4)} }{\text{(average loss to layer s.t. loss xs 1)}}$$ i.e. the price for the 6 xs 4 is the price for the 9 xs 1 multiplied by the probability of a loss being excess 4, scaled by the quotient of the average loss into each layer. In this case, we have: $$\text{Price}_{\text{6 xs 4}} = 10m* 22\% \frac{2,136,364}{1,490,000} = 3,154,362$$ |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
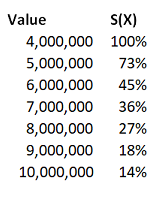
 RSS Feed
RSS Feed
Leave a Reply.