Drinking Game Analysis3/3/2018
When you are playing a drinking game, do you ever catch yourself calculating the probabilities of various events happening? If you are like most people the answer to that is probably "..... um..... no....... why would I ever do that...."
Okay, maybe that's not the kind of thing you think about when playing a drinking game. But I bet you think it would be interesting to know what the odds are anyway? No? Really? Still not that interested? .... Okay... well I find it interesting, so I'm going to write about it anyway. Eyes up/Eyes down I've only played this game a couple of times but it's pretty fun, it requires no equipment, and has quite a lot of drinking. All players sit in a circle, one player calls out "Eye's down" at which point everyone looks down, the same player then says "Eye's up" at which point everyone looks up at a random person in the circle. If the person you are looking at is also looking at you, then you both drink. Pretty simple. What is the probability that you will drink? Let's denote the event that you have matched someone with $M$. Then: $$P(M) = \frac{1}{n-1} $$ Where $n$ is the number of players.
To see that this is true, assume that everyone is picking a random person to look at, then it shouldn't matter who you are looking at, that person will always have $n-1$ people to pick from, and therefore a $ \frac{1}{n-1} $ chance of looking at you.
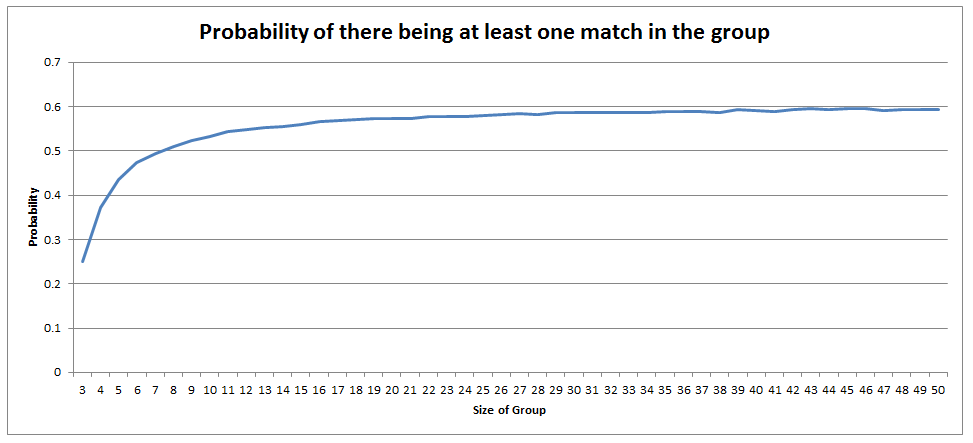
Of course people in real life tend not to pick a random person to look at, and even if they attempt to pick a random person, people have been shown to be terrible at picking randomly. But for the purposes of this analysis, unless we make this assumption, the only alternative would be to play the game hundreds of times, record how often matches are made, and then make an empirical claim. As fun as it sounds to play this game hundreds of times in a row, it would be better for your health to just assume a uniform spread of guesses. The fact that you have a $ \frac{1}{n-1} $ chance of getting a match means that the more people are playing the game, the less likely each person is to drink. Does this apply to the group as a whole though? What is the probability that someone in the group drinks? If we had a hundred people playing, then each individual would hardly ever drink. In fact you would expect them to drink once every $99$ goes. But would you expect it to also be unlikely that anyone at all drinks? I spent about an hour trying to calculate this and didn't get very far. Calculating through conditional probabilities doesn't seem to help, and I couldn't come up with a decent approach to count the permutations of all the possible ways of selecting pairings for elements in a set, such that there are no 2-cycles. In the end I gave up and just wrote a program to calculate the answer stochastically. Monte Carlo analysis really is such a versatile tool for problems like these. Anytime you can formulate the problem easily, but struggle to come up with an analytical solution, Monte Carlo analysis will probably work. Here is the table I generated of the probability of someone in the group drinking for a group of size n:
There is a definite trend here, if we plot the values on the chart it looks pretty clear that out solution converges to $0.6$. No idea why though! I might come back to this problem another time, but if anyone has any thoughts then please let me know.
Odds So this is not technically a drinking game, but is played quite often by people who are out drinking. The rules for this game are pretty simple, anytime you would like to dare someone to do something you say "odds of you doing this". The dare might be anything, from 'eating a spoon full of chilli powder, downing your drink, or even getting a tattoo (that last one is a real one I heard about from a friend who playing the game while travelling in Eastern Europe). The person you have challenged then gives you a number. They might say $20$, then each of you count down from $3$ and say an integer from $1$ to $20$ (or whatever number they selected). If you both said the same number, then they have to do the dare. Therefore the higher number you pick, the less likely it is that you will have to do the dare. What are the odds of you having to do whatever it is you are betting on, based on you selecting the number $n$? This is quite a straightforward problem, the answer is just $\frac{1} {n} $. I was playing this game last week with someone who thought the answer might be $\frac{1} {n^2} $. This would give a very different likelihood of having to do the dare. For example if you selected $20$, then you would have a $5 \%$ chance of having to do the dare, but according to my friend's calculation he thought you would have $0.25 \%$ chance of doing the dare. Here is a table showing the correct probabilities for various values of $n$. Dirty Pint Flip I wouldn't recommend playing this game to be honest. I played it in uni once, but it's a bit grim. All the players sit in a circle with a central pint glass in the middle, the players take it in turn to pour any amount of their own drink into the central pint glass as they would like, they then have to flip a coin and guess whether it will be heads or tails. If they get it right, then the game moves on to the person to their left, if they get it wrong, then they have to down the dirty pint. When I played it some people were drinking wine, some people were drinking beer... it was not a good combination. What is the probability that you will have to drink? This is quite straight forward, it is simply the probability that you will guess the coin flip correctly. Which is just $\frac{1}{2} $. What about the question of how much you will drink on average? That is, on average if you have to drink, how many people will have poured their drink into the glass before you drink? We can model this as a geometric distribution and calculate the probabilities of each possible number of people. Let's denote the number of people who have poured in before you, given you are about to drink as $N$, then:
$$N \sim Geo(0.5) $$
Giving us the following table: The expected value of the number of drinks is then the sumproduct of these two columns . This gives us a value of $2$. Therefore, if you have to drink, the average number of drinks that will have been poured into the pint is $2$. Two Dice Nominate This is another game I've only played a couple of times. And I'm not sure if it has a better name than the one I've given it, if you know of one then let me know. In this game, you sit in a circle with a range of drinks on the table, you take it in turns to nominate a person, a drink, and a number between $2$ and $12$. You then roll two dice and add them together. If you have rolled the correct number, the person you nominated drinks the drink you selected, if however you roll a double, then you drink that drink. If it is both a double and you get it correct, then you both have to drink. The reason that this game does not have much depth to it is that you can always just pick the most likely number to come up when rolling two dice. Here is a table showing the probability of each value coming up: Therefore you might as well pick $7$ every single time! Is there anything else we can say about this game? We know that if we roll a double, then we have to drink the drink. What is the probability of you rolling a double in this game? The probability of this is always just $\frac{1}{6} $. Interesting this is the same probability as rolling the dice such that the sum is $7$. Therefore, if you do pick $7$, there is an equal chance of you and the person you are nominating drinking the drink. |
AuthorI work as an actuary and underwriter at a global reinsurer in London. Categories
All
Archives
April 2024
|
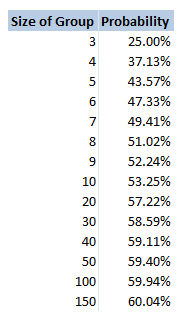
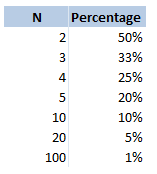
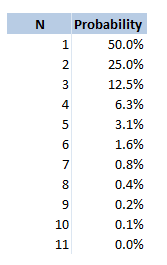
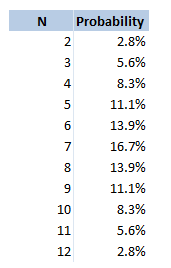
 RSS Feed
RSS Feed
Grateful ffor sharing this
Leave a Reply.