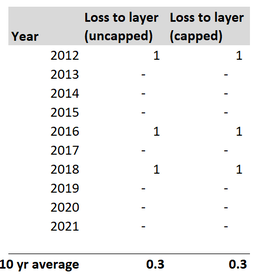
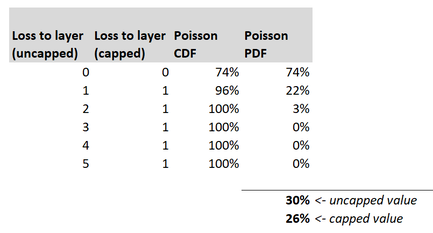
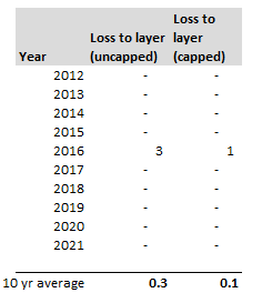
Capped or uncapped estimators

I was reviewing a pricing model recently when an interesting question came up relating to when to apply the policy features when modelling the contract. 

Source: Dall.E 2, Open AI. 

​I thought it would be fun to include an AI generated image which was linked to the title 'capped vs uncapped estimators'. After scrolling through tons of fairly creepy images of weird looking robots with caps on, I found the following, which is definitely my favourite - it's basically an image of a computer 'wearing' a cap. A 'capped' estimator...

We were pricing a layer, let's call it 1m xs 4m, with no reinstatements (i.e. single shot). We had the following historic losses to layer, on a trended and developed basis. (for now, don't worry about trend rate, dev factors, etc.):

​

The first column represents the loss to layer without applying the benefit of the single shot feature. The second column represents the loss to layer with the benefit of the fact that we can only have at most 1m of loss per year. Note that the two columns are the same, as in the past we only had a max of 1 loss per year anyway, even before applying the annual cap.

Based on the uncapped column, our value for the 10 year burn is 0.3. i.e. if we wished to estimate the expected value of the uncapped loss to layer next year, then 0.3 would be a sensible starting point. And given the layer in question does have a cap, standard practice would be to take this value of 0.3, and then stochastically model the benefit of the single shot feature.

To do this, we would parameterise a Poisson distribution (or possibly negative binomial, but let's just use Poisson to keep the maths easier) with lambda = 0.3, and then calculate the capped loss to layer. And in fact, this version is simple enough that we could do it analytically, rather than needing to use a Monte Carlo simulation. Here is the relevant table:

The 0.3 is simply the expected value of the uncapped losses, calculated as the sumproduct of the pdf and the uncapped loss to layer. The 0.26 is the expected value of the capped loss to layer, calculated as the sumproduct of the pdf and the capped loss to layer. So we can see that our capped value = 0.26. And this would be a sensible starting point for the expected capped loss to layer for next year. 

But isn't this strange? (and this was the question that was posed to me by a colleague). Historically the actual burn to layer, with benefit of the single shot was 0.3 as per the first table. But now you're telling me the correct value = 0.26? 

What was the alternative to the 0.26 value my colleague was suggesting? Well, we could simply take 0.3 as our value for the capped estimator, which was the actual historic average with the benefit of the cap, and not bother with any stochastic adjustments at all.

So why is this first method justified over the seemingly simpler alternative? Can we motivate it somehow?

Motivation
​
We need to think about applying the pricing process stochastically across a portfolio. Let's refer to modelling the uncapped estimator, and then stochastically calculating the capped value as the 'uncapped' method. And the alternative of just directly calculating the capped values as the (very imaginatively named) 'capped' method.

Consider the consequence of running either the capped or uncapped methods on a range of datasets. For example, suppose the historic results were as per the below table, rather than the table we orginally started with.

Note that we've still got a total of 3 events in 10 years, so our uncapped estimator is once again 0.3, but now our uncapped estimator is 0.1. A massive drop vs 0.3 last time.

And this should neatly illustrate the main benefit of the uncapped method. For a given uncapped frequency, we get the same value for the capped frequency, no matter how the events fell across the 10 years. Because if we were to apply the uncapped method to the 2nd table, we'd still have 0.3 as our uncapped estimator, and then 0.26 as our expected capped value.

Now you might respond - isn't there info in exactly how the events fell which you are then discarding when replacing with a known frequency distribution? And this is true - but this shouldn't effect how we estimate the uncapped estimator. This is more of a consideration for which frequency distribution to use when doing the stochastic step to infer the benefit of the single shot feature. Another way of saying this is that by using the capped method, we are effectively always using the empirical frequency distribution when modelling the single shot feature. 

Another way to motivate the first method is from an information theory perspective - the uncapped method uses all the available loss data, and therefore we should have a preference towards using it compared to a method that immediately starts throwing away data, by just looking at the capped values.

As an aside, I'm actually quite sympathetic to using the empirical distribution in cases where the sample has sufficient volatility, and we are not predicting out of sample. It's a bit of a bug bear of mine when people do convoluted calculations to fit some random curve with 5-parameters just to get as close a fit to the empirical distribution as possible, and then not actually do anything out of sample anyway. Why not just use the empirical distribution? Sure you get a more graduated curve, but is it more accurate? I'm not convinced.

Another interesting angle on this question is the fact that the original model I was reviewing was a bespoke model for a one-off large risk. In this case, is it still valid to think of the pricing process stochastically in terms of multiple datasets when you won't actually ever repeat this exact analysis? This is more of a philosophical approach question - I would say yes - because you're still hopefully going to build a portfolio out of multiple unique bets. Each might be unique, but hopefully if you use statistically unbiased methods for each one, then at a portfolio level we should be happy.

Conclusion

So have we convinced ourselves that we should prefer the uncapped method? We've given a couple of arguments in its favour, and hopefully they are somewhat convincing, but I don't think either is so compelling that we can really say the capped method is 'incorrect' in any strong sense of the word.